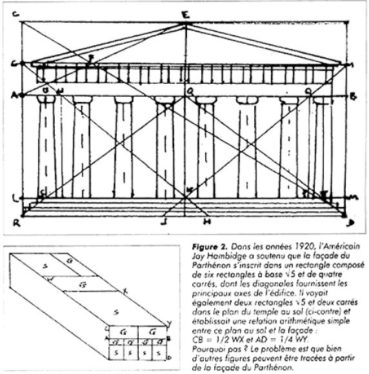
Mathématiques et botanique : nombre d’or, angle d’or, suite de Fibonacci et phyllotaxie
Title
Mathematics and botany: golden ratio, golden angle, Fibonacci sequence and phyllotaxis
Résumé
Des mathématiques à la botanique est un article de vulgarisation en trois parties. Dans la première, compréhensible par un bachelier scientifique, l’auteur aborde les définitions et les étonnantes propriétés mathématiques conjointes du nombre d’or, de l’angle d’or, de la suite de Fibonacci et des spirales les plus connues. Dans la deuxième, il expose les connaissances actuelles sur la phyllotaxie – description de la disposition des feuilles sur la tige d’une plante, des fleurs dans ses inflorescences et des pièces florales de ses fleurs – et le lien étroit entre la phyllotaxie et les notions mathématiques précédentes. Dans la troisième, il donne des éléments pour mieux comprendre le mythe moderne qui voudrait que le nombre d’or ait été connu et universellement utilisé, depuis l’Antiquité, comme canon de beauté et d’harmonie dans l’architecture et dans les arts. Un glossaire contient de nombreuses définitions et des compléments de mathématiques et de botanique utiles à la bonne compréhension du texte.
Abstract
From Mathematics to Botany is a three-part article for the public at large. In part one, which can be understood by anyone with a BSc (or its equivalent), the author discusses the definitions and the amazing and associate mathematical properties of the golden ratio, the golden angle, the Fibonacci sequence and some of the best-known spirals. In part two, he presents our current knowledge of phyllotaxis – i.e. a description of how leaves on a plant stem of a plant are arranged, inflorescences and the floral parts of its flowers – and the close link between phyllotaxis and previous mathematical notions. In part third, he provides elements for a better understanding of the modern myth that the golden ratio has been known and universally used, since Antiquity, as a canon of beauty and harmony in architecture and the arts. A glossary contains numerous definitions plus mathematical and botanical supplements useful for a better understanding of the text.
Notes préalables – Les noms scientifiques des espèces végétales sont cités sans mention de leurs auteurs. Pour les espèces de France métropolitaine, voir Tison & de Foucault (2014). Pour les espèces exotiques, les noms ont été relevés sur le site internet Wikipedia. En annexe, un glossaire donne de nombreuses définitions et des compléments. Pour les symboles mathématiques, la police du module Symbole de Word est Cambria Math, un peu différente de la police Arial utilisée dans le reste du texte ; ces petites différences de forme ne devraient pas gêner la lecture et la compréhension.
PARTIE I
Nombre d’or, angle d’or, spirales et suite de Fibonacci en mathématiques
1. L’héritage de l’Antiquité
1.1. Les nombres, révélateurs de l’harmonie du monde dans les civilisations antiques
Dans toutes les grandes civilisations antiques qui se sont développées dans le triangle formé par la Mésopotamie, l’Égypte et la Grèce, l’origine du monde était expliquée par une intervention divine et les humains ne pouvaient qu’entrevoir, ou du moins le pensaient-ils, le dessein du créateur et ce qu’il attendait d’eux. Les savants de l’Antiquité – à la fois mathématiciens, philosophes, astronomes, astrologues, mages et poètes – étaient fascinés par la régularité et la périodicité de leurs observations astronomiques, par les invariances et les symétries observables dans la nature, mais aussi, en particulier dans la Grèce antique, par les figures géométriques régulières et les propriétés arithmétiques des nombres entiers que, pensaient-ils, les dieux leur laissaient découvrir.
1.2. Les observations astronomiques, leur interprétation scientifique ou religieuse
Depuis les temps les plus reculés, les humains ont observé le ciel. Dans l’Antiquité proche-orientale, le ciel était vu comme une voûte céleste centrée sur la Terre et tournant autour d’elle.
À cette époque, les cieux étaient considérés comme lieu de résidence de Dieu ou des dieux, un lieu à la fois inaccessible et très proche de la surface terrestre, que l’on pouvait approcher en gravissant les plus hautes montagnes. Dans la mythologie grecque, le mont Olympe (2 917 m) était le domaine des dieux. Dans la Bible, l’arche de Noé aurait retrouvé la terre ferme au sommet de l’inaccessible mont Ararat (5 165 m) et Jacob voit en rêve une échelle reliant le ciel et la terre, qui lui permet d’accéder au ciel et de voir Dieu, lequel renouvelle l’Alliance conclue avec l’humanité. Les premiers mots du Notre Père chrétien, Notre Père, qui es aux cieux…, ne sont plus pris au pied de la lettre, mais ils l’étaient par le passé : les peintures de Michel-Ange au plafond de la chapelle Sixtine représentent Dieu entouré d’anges dans les cieux.
Les observations astronomiques étaient indissociables des interprétations magiques ou religieuses qui en étaient faites. Les phénomènes périodiques que chacun de nous peut observer – alternance et durée du jour et de la nuit au cours du cycle annuel des saisons, trajectoires apparentes du Soleil, de la Lune et des planètes, phases de la Lune, cycles de déplacement global des étoiles – étaient évidemment connus, mais leur interprétation était très différente de celle que nous en faisons actuellement.
Les positions relatives des astres et des étoiles étaient interprétées comme des messages divins, permettant aux humains d’entrevoir leur avenir. Les phénomènes rares ou exceptionnels – éclipses de Lune ou de Soleil, conjonctions de planètes, passage d’une comète ou, encore plus rare, explosion d’une supernova – annonçaient des évènements tout aussi exceptionnels, comme le début d’une ère nouvelle, ou servaient d’avertissement avant une catastrophe de grande ampleur.
Enseignement secret réservé aux seuls initiés, mélange d’observations astronomiques et d’interprétations ésotériques, ces croyances scientifiquement infondées sont toujours les bases de l’astrologie (voir glossaire) et de la numérologie. L’astrologie occidentale, qui trouve ses origines en Mésopotamie, entre le xixe siècle et le xviie siècle av. J.-C., est une croyance qui repose sur la position, variable en fonction de la date au cours d’une année, de douze constellations (chacune partagée en trois décans) que l’on observe dans le zodiaque, bandeau circulaire de la voûte céleste centré sur le plan écliptique.
D’autres civilisations ont développé des interprétations astrologiques à partir de leurs propres observations astronomiques : les Chinois (vers 2 600 av. J.-C.), les Hindous, les Mayas.
Les savants de l’Antiquité distinguaient, sur la voûte terrestre qu’ils voyaient tourner autour de la Terre, sept « astres » mobiles les uns par rapport aux autres, mais pas tous visibles simultanément, et d’innombrables étoiles, fixes les unes par rapport aux autres mais se déplaçant en bloc.
Dans l’Antiquité, sept est le nombre des merveilles du monde et des collines de Rome, et il apparaît à de multiples reprises dans la Bible, dans les Évangiles et dans le Coran. De nos jours, sept est le nombre de jours de la semaine, respectivement dédiés à l’un de ces sept astres : dimanche est (ou était) dédié au Soleil (Sunday en anglais), lundi à la Lune, mardi à Mars, mercredi à Mercure, jeudi à Jupiter, vendredi à Vénus et samedi à Saturne. Il se retrouve dans les traditions populaires, les jeux (comme le « jeu des sept familles »), les romans, les contes, les films, les bandes dessinées…
Mais ce n’est pas tout : il y a au moins cinq mille ans, les savants sumériens avaient remarqué que le nombre de jours dans l’année solaire est proche de 360. Par un heureux hasard, 360 est, parmi tous les nombres de taille comparable, celui qui possède le plus de diviseurs entiers, propriété appréciable à une époque où la division de deux nombres n’était envisageable que lorsque le résultat était un nombre entier. En répartissant 360 petits cailloux (calculus en latin…) en tas d’un même nombre d’éléments, on constate que 360 est égal, à l’ordre près des facteurs, à 2 × 180, 3 × 120, 4 × 90, 5 × 72, 6 × 60, 8 × 45, 9 × 40, 10 × 36, 12 × 30, 15 × 24, 18 × 20, ce qui prouve que 360 possède 22 diviseurs propres, d’où l’adoption, en Mésopotamie, il y a environ cinq millénaires, d’un système de numération de position en base 60, la numération sexagésimale, encore utilisé de nos jours pour mesurer les durées de temps et les angles.
Pour les durées de temps, tout serait plus simple si l’année comptait exactement 360 jours solaires, mais ce n’est pas le cas : une année solaire, initialement définie à partir des équinoxes ou des solstices, compte actuellement 365,242 jours. Depuis l’Antiquité et du fait qu’elle ne correspond pas à un nombre entier de jours, l’année solaire a été divisée en douze mois d’environ trente jours, la dérive annuelle des dates par rapport aux équinoxes et solstices étant compensée par des années bissextiles. Simultanément, elle a été divisée en quatre saisons de trois mois chacune et chaque jour est divisé en 24 heures, chacune de soixante minutes, chacune de soixante secondes. Chez de nombreuses civilisations, solstices et équinoxes étaient (et sont encore) l’occasion de célébrations : en Europe occidentale, les feux de la Saint-Jean en sont un exemple.
Parallèlement, certaines civilisations ont adopté un calendrier lunaire. Est-ce plus simple ? Pas vraiment, car l’année solaire ne correspond pas à un nombre entier de lunaisons. Vue depuis le centre du Système solaire (mois lunaire sidéral), la Lune tourne actuellement autour de la Terre en 27 jours, 7 heures, 43 minutes et 11,5 secondes. Pendant ce temps, la Terre parcourt un peu moins qu’un douzième de son orbite, parcourue dans le même sens que la Lune sur la sienne : vue depuis la Terre, la même phase de la Lune (lunaison) s’observe actuellement au bout de 29 jours, 12 heures, 44 minutes et 2,8 secondes (soit 29,531 jours). C’est pour cela que le calendrier islamique – fondé sur l’observation des lunaisons – compte 12 mois de 29 ou 30 jours, pour un total de 354 ou 355 jours. Comparée à l’année solaire, cette année lunaire est plus courte d’environ onze jours et, année après année, décalée d’autant par rapport aux saisons. Autre particularité de ce calendrier, la date (et l’heure) de début du mois est fixée par l’observation directe, à l’œil nu, de la nouvelle lune. De ce fait, elle dépend de la longitude du lieu d’observation. Dans l’Église catholique, la date de Pâques est également fixée d’après un calendrier lunaire.
La mesure des angles, liée depuis les origines à la définition de l’année solaire, se fait aussi en base sexagésimale. Dans un cercle, l’angle au centre qui intercepte le cercle entier mesure 360° et les angles mesurés dans les polygones réguliers usuels (triangles, carrés, pentagones, hexagones, etc.) sont des diviseurs entiers de 360. Pour la navigation maritime et aérienne, les mesures internationales de longitude et de latitude sont aussi exprimées en degrés sexagésimaux. Cependant, en mathématiques, les calculs sont bien plus simples lorsque les angles sont mesurés en radians.
2. Le nombre d’or
2.1. Euclide et Pythagore : la « section dorée », ou « division d’un segment en extrême et moyenne raison »
Les philosophes grecs étaient convaincus que la création du monde était régie par les seuls nombres entiers naturels (un, deux, trois, etc., mais pas encore zéro) et leurs rapports simples (un demi, un tiers, deux tiers, un quart, trois quarts, etc.).
Le terme de philosophe était employé par Pythagore, qui ne se présentait pas comme un sage, mais comme un « ami de la sagesse », où sagesse désignait un idéal de vie réservé aux seuls initiés. Comme actuellement, les qualités d’un sage reposaient sur la connaissance, le savoir et l’expérience acquise. La mathématique, littéralement « ce qui peut être appris et enseigné », était une partie essentielle de cette sagesse, comme le rappelle la phrase, attribuée à Platon, qui aurait été gravée à l’entrée de l’Académie : « Nul n’entre ici s’il n’est géomètre ».
Les fondements de la mathématique étaient arithmétiques et géométriques : les nombres et les règles de calcul sur les nombres dérivaient des propriétés géométriques liées à la mesure des longueurs, des aires et des volumes. Les calculs algébriques, tels que nous les connaissons actuellement, n’ont été codifiés qu’à partir du xvie siècle, longtemps après la publication, vers 825, de l’ouvrage fondateur du mathématicien d’origine persane Al-Khwarismi : le titre de cet ouvrage a donné le mot « algèbre » et le nom de son auteur a donné « algorithme ».
Dans l’Antiquité et jusqu’au xvie siècle, la résolution de problèmes conduisant à des équations du premier ou du second degré utilisait des méthodes de calcul et des algorithmes (qui ne s’appelaient pas encore ainsi) bien plus complexes pour nous que le calcul algébrique codifié actuel. Essayez de refaire, sans utiliser les notations actuelles, les calculs sur les fractions égyptiennes donnés en exemples dans le glossaire. Comprenez-vous facilement les traductions des passages de De Divina Proportione, livre de Luca Pacioli et Léonard de Vinci publié en 1509, données par Fernando Corbalán dans son ouvrage sur le nombre d’or ?
Ces philosophes s’intéressaient à de nombreuses régularités, tout particulièrement :
- aux proportions, rapports de longueurs, d’aires ou de volumes donnant une impression d’harmonie, d’équilibre artistique ou architectural ;
- aux divisions d’un segment dans une proportion donnée, s’exprimant comme quotient de deux entiers et à même d’être reproduites à l’identique à différentes échelles ;
- aux suites additives, en particuliers aux suites arithmétiques, dans lesquelles on passe d’un terme au suivant par addition d’un nombre constant appelé « raison » ; le mot raison a pour racine le mot latin ratio, qui désignait de manière générale un calcul ; on comparera le mot « raison » (d’une suite arithmétique) au mot « ration », de même étymologie, qui désigne la portion journalière de nourriture attribuée à chaque soldat en campagne ;
- aux suites multiplicatives, en particulier aux suites géométriques, dans lesquelles on passe d’un terme au suivant en le multipliant par un nombre constant, lui aussi appelé « raison » ; le qualificatif de « géométrique » vient de ce que, dans l’Antiquité grecque, la multiplication était indissociable des calculs d’aires ou de volumes. Le produit x x y est l’aire d’un rectangle de côtés x et y. Nous disons toujours « x au carré » pour x2 = x x x, aire d’un carré de côté x, ainsi que « x au cube » pour x3 = x x x x x, volume d’un cube d’arête x.
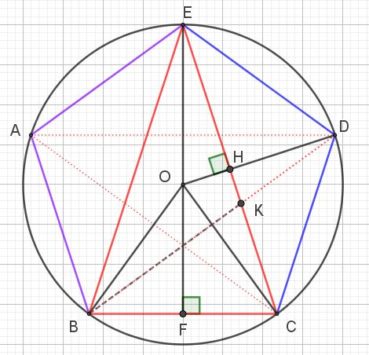
Dans ses Éléments de Mathématique, rédigés aux environs de 300 avant J.-C., Euclide décrit plusieurs partages d’un segment dans une proportion donnée, dont la « division d’un segment en extrême et moyenne raison », ou « section dorée ». Dans cette division, un segment de longueur a+b, avec a > b, est découpé de manière à ce que, avec les notations actuelles, très différentes de celles qu’utilisait Euclide :
![]()
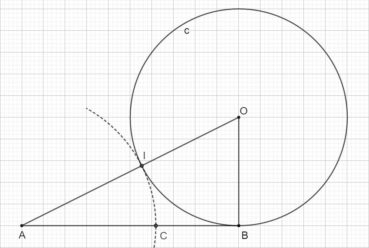
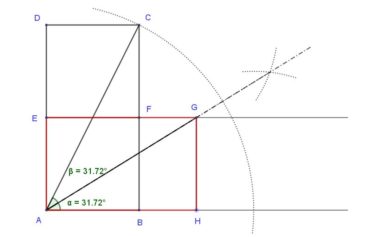
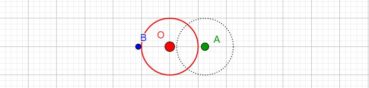
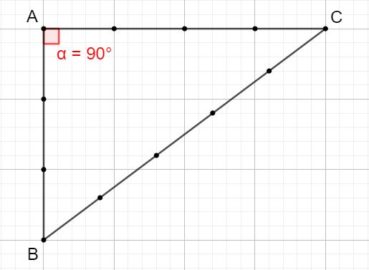
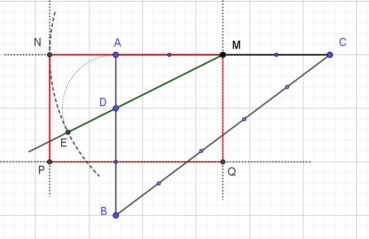
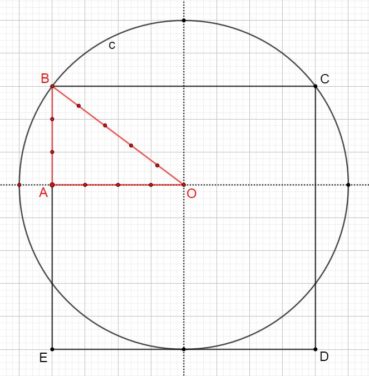
Voici comment construire la division d’un segment en extrême et moyenne raison par la méthode d’Euclide (figure 1) :
- construire un triangle rectangle ABO, rectangle en B, tel que OB = 1/2 AB ;
- construire le cercle de centre O et de rayon OB, qui coupe le segment [AO] en I ;
- construire l’arc de cercle de centre A passant par I, qui coupe le segment [AB] en C.
Alors AB/AC = AC/CB. Essayez de le démontrer ! (indications page 91).
2.2. L’équation qui définit le nombre d’or
Le nombre d’or, habituellement noté φ (lettre grecque « phi »), est la valeur numérique commune des quotients (a+b)/a et a/b dans la division d’un segment en extrême et moyenne raison. La relation (a+b)/a=a/b peut s’écrire a/a+b/a=a/b. Alors 1+1/φ=φ. En multipliant les deux termes par φ, on obtient φ+1=φ2, ce qui montre que φ est solution de l’équation trinôme du second degré : φ2-φ-1=0. Cette équation s’écrit φ(φ-1)=1. On déduit que les nombres φ et φ-1 sont inverses l’un de l’autre : φ-1=1/φ et φ=1/φ-1.
Les lycéens qui savent résoudre cette équation lui trouvent deux solutions : la première est ![]() , de valeur numérique approchée 1,618, et la seconde est
, de valeur numérique approchée 1,618, et la seconde est ![]() , de valeur numérique approchée – 0,618. Nombre positif car quotient de deux nombres positifs, φ ne peut être que la première de ces deux solutions :
, de valeur numérique approchée – 0,618. Nombre positif car quotient de deux nombres positifs, φ ne peut être que la première de ces deux solutions : ![]() . Un calcul simple montre que
. Un calcul simple montre que ![]()
2.3. Le nombre d’or, nombre incommensurable
Pour les philosophes de la Grèce antique, un nombre incommensurable était un nombre qui, une unité étant choisie, apparaissait dans la mesure d’une longueur sans être un nombre entier ni le rapport de deux nombres entiers. Cette propriété définit actuellement un nombre irrationnel.
Le premier nombre irrationnel découvert est ![]() qui, en application du théorème de Pythagore, mesure la longueur de la diagonale d’un carré de côté unité. La preuve de son irrationalité – qui repose sur des propriétés de divisibilité des nombres entiers et un raisonnement par l’absurde – est attribuée à l’école de Pythagore, en particulier à Hippase de Métaponte (vie siècle av. J-C.). Celui-ci aurait également découvert une construction du pentagone régulier à la règle et au compas faisant intervenir la section dorée, donc le nombre d’or φ, et aurait prouvé que φ est un nombre irrationnel (voir « géométrie du pentagone », pages 8 à 12).
qui, en application du théorème de Pythagore, mesure la longueur de la diagonale d’un carré de côté unité. La preuve de son irrationalité – qui repose sur des propriétés de divisibilité des nombres entiers et un raisonnement par l’absurde – est attribuée à l’école de Pythagore, en particulier à Hippase de Métaponte (vie siècle av. J-C.). Celui-ci aurait également découvert une construction du pentagone régulier à la règle et au compas faisant intervenir la section dorée, donc le nombre d’or φ, et aurait prouvé que φ est un nombre irrationnel (voir « géométrie du pentagone », pages 8 à 12).
La découverte de l’irrationalité de ![]() , puis celle de l’irrationalité du nombre d’or φ et le fait que φ soit lié à la construction du pentagone régulier ont profondément déstabilisé les philosophes de l’école pythagoricienne. Persuadés jusqu’alors que le monde n’était régi que par les nombres entiers et leurs rapports, ils voyaient leur explication de la création du monde s’écrouler. Mais, en même temps, ils venaient de découvrir l’un des secrets des dieux, ce qui ne pouvait qu’entretenir le mystère autour de leurs connaissances.
, puis celle de l’irrationalité du nombre d’or φ et le fait que φ soit lié à la construction du pentagone régulier ont profondément déstabilisé les philosophes de l’école pythagoricienne. Persuadés jusqu’alors que le monde n’était régi que par les nombres entiers et leurs rapports, ils voyaient leur explication de la création du monde s’écrouler. Mais, en même temps, ils venaient de découvrir l’un des secrets des dieux, ce qui ne pouvait qu’entretenir le mystère autour de leurs connaissances.
Depuis, pour certains, le mystère ne s’est toujours pas dissipé : le nombre d’or et ses multiples propriétés, le pentagone régulier et le pentagramme ont conservé ce caractère mystérieux, objet de nombreuses interprétations plus ou moins ésotériques. Il suffit de parcourir le web pour mesurer à quel point cette vision est encore bien présente, mais ce qui suit incitera peut-être à prendre un peu de recul face à certaines affirmations…
Les philosophes grecs ont vainement cherché la valeur rationnelle d’un autre nombre qui échappait à leur entendement, le nombre π, rapport du périmètre d’un cercle à son diamètre. Ils espéraient trouver une valeur rationnelle de π en résolvant le fameux problème de la quadrature du cercle, qui consiste à construire, à la règle et au compas, un carré de même aire que celui d’un cercle donné. L’impossibilité de cette construction et l’irrationalité du nombre π n’ont été prouvées qu’au xviiie siècle, en 1767, par Jean-Henri Lambert. L’approximation rationnelle la plus simple de π est 3, mais les approximations par 25/8 et 22/7 sont bien meilleures :
![]() , alors que
, alors que ![]() et que
et que ![]()
2.4. Le nombre d’or sous forme de racine continue et de fraction continue
Comme φ est un nombre positif, la relation φ² = φ + 1 conduit à ![]() Partant de cette relation, que l’on reporte récursivement dans elle-même et jusqu’à l’infini, on obtient la plus simple des racines continues :
Partant de cette relation, que l’on reporte récursivement dans elle-même et jusqu’à l’infini, on obtient la plus simple des racines continues :
![]()
![]()
![]()
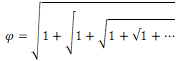
Mais une racine continue ne se prête guère au calcul.
Partant de ![]() , que l’on reporte récursivement dans elle-même jusqu’à l’infini, on obtient la plus simple des fractions continues :
, que l’on reporte récursivement dans elle-même jusqu’à l’infini, on obtient la plus simple des fractions continues :
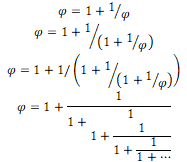
Cette propriété implique que φ est le plus irrationnel des nombres irrationnels et explique pourquoi le nombre d’or intervient dans la phyllotaxie des végétaux (voir page 45). Pour expliquer la raison de cette « super-irrationalité », rappelons deux propriétés des nombres réels :
- si un nombre réel n’est pas entier, son développement décimal peut être décomposé en somme de sa partie entière et d’un reste supérieur à 0 et strictement inférieur à 1 ;
- si ce reste n’est pas nul, et c’est toujours le cas lorsque le nombre est irrationnel, il possède un inverse.
Appliquons ces propriétés au nombre irrationnel le plus connu, le nombre π, en partant de son approximation décimale (les pointillés signalent des décimales manquantes) :
![]()
![]()
![]()
![]()
Nous venons de trouver le début de la fraction continue qui représente le nombre π. Dans celle-ci, les dénominateurs entiers des restes successifs forment la « suite des réduites » du nombre , notée [3, 7, 15, 1, 292…], qui caractérise le nombre développé. Le calcul des réduites successives permet d’obtenir des valeurs approchées de ce nombre, de plus en plus précises puisqu’on néglige des restes de plus en plus petits. Calculons les cinq premières réduites de π : [3], [3, 7], [3, 7, 15], [3, 7, 15, 1], [3, 7, 15, 1, 292] :
![]()
![]()
![]()
![]()
![]()
Le calcul des cinq premières réduites permet d’obtenir neuf décimales exactes de π.
De manière générale, pour tout nombre irrationnel représenté par sa fraction continue, le nombre de réduites à calculer pour obtenir une bonne approximation est d’autant plus petit que les termes de la suite des réduites sont grands. A contrario, plus ces termes sont petits, plus le nombre de réduites à calculer est grand.
La relation
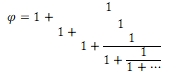
montre que les réduites correspondantes sont toutes de la forme [1, 1, 1, 1, 1…], et aucune suite de réduites ne peut être plus simple : φ est bien le plus irrationnel des nombres irrationnels.
Les calculs, détaillés pages 16, montrent qu’il faut calculer seize réduites de ![]() pour obtenir six décimales exactes alors que, nous venons de le voir, il suffit de calculer cinq réduites de pour obtenir neuf décimales exactes : φ est bien plus irrationnel que π !
pour obtenir six décimales exactes alors que, nous venons de le voir, il suffit de calculer cinq réduites de pour obtenir neuf décimales exactes : φ est bien plus irrationnel que π !
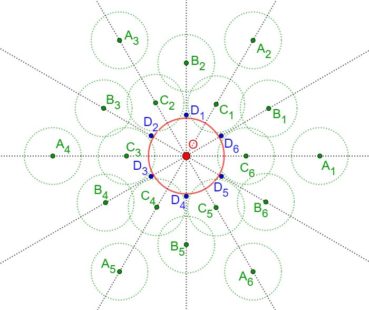
3. L’angle d’or
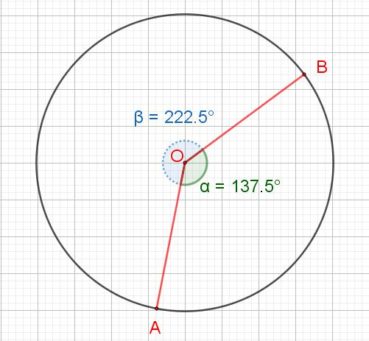
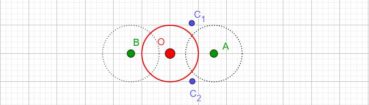
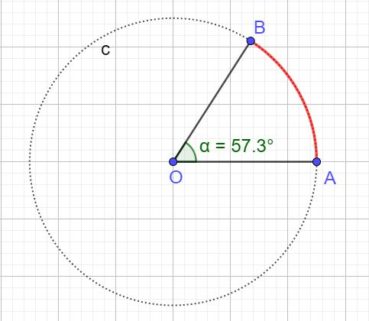
Dans un cercle, l’angle d’or (figure 2) est un angle au centre qui intercepte le plus petit des deux arcs qui partagent la circonférence en extrême et moyenne raison :
![]()
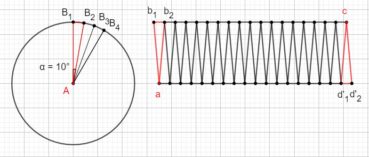
En prenant comme unité le rayon du cercle, les mesures en radians des angles α et β doivent vérifier α + β = 2π et 2π/β = β/α = φ, ce qui implique que β = α x φ donc que α = β/φ. De 2π/β = φ, on déduit que β = 2π/φ et enfin que α = 2π/φ2 radians. En degrés, ces angles ont pour mesures respectives α=360°/φ2, de valeur approchée 137,5°, et β=360°/φ2, de valeur approché 222,5°. Par la suite, nous utiliserons comme mesure de α la valeur approchée 137,5°, et nous verrons que, chez les plantes à phyllotaxie spiralée, les feuilles sur la tige, les fleurs sur l’inflorescence ou les pièces florales se forment selon un processus autosimilaire qui utilise les propriétés de cet angle.
4. Le rectangle d’or
4.1. Format d’un rectangle, exemple du format A
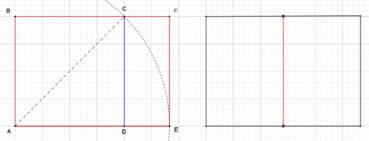
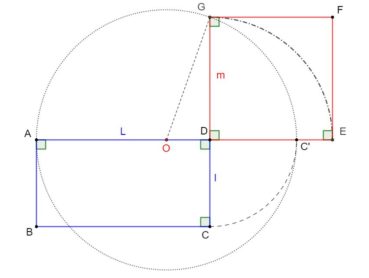
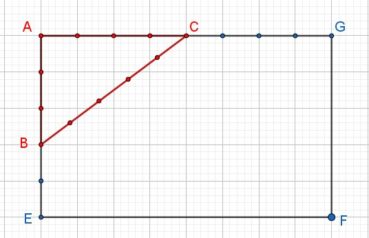
Le format d’un rectangle est le quotient de sa longueur par sa largeur. Le format de papier actuellement le plus utilisé dans le monde est le format A, décliné en feuilles de format A0, A1, A2, A3, A4, A5, etc. Le rapport longueur/largeur de toute feuille de format A est égal à ![]() , ce qui permet de la partager en deux feuilles de même format et d’aire moitié. Par définition, l’aire d’une feuille de format A0 est égale à 1 m². En valeurs arrondies, elle mesure 1 189 mm de longueur pour 841 mm de largeur. La figure 3 donne la construction d’un rectangle au format A :
, ce qui permet de la partager en deux feuilles de même format et d’aire moitié. Par définition, l’aire d’une feuille de format A0 est égale à 1 m². En valeurs arrondies, elle mesure 1 189 mm de longueur pour 841 mm de largeur. La figure 3 donne la construction d’un rectangle au format A :
- à gauche, dans un carré ABCD de côté unité, la diagonale [AC] a pour longueur
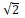 . L’arc de cercle de centre A et de rayon AC coupe la demi-droite [AD] en E : le rectangle AEFB est au format A ;
. L’arc de cercle de centre A et de rayon AC coupe la demi-droite [AD] en E : le rectangle AEFB est au format A ; - à droite, la médiatrice de [AE] partage ce rectangle en deux rectangles de même format A, puisque
 .
.
Les propriétés du format A sont les suivantes :
- à l’aide d’une photocopieuse, par agrandissement d’un facteur
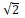 (pourcentage approché d’agrandissement 141 %), on passe d’une feuille de format A4 à une feuille de format A3 ; par réduction d’un facteur
(pourcentage approché d’agrandissement 141 %), on passe d’une feuille de format A4 à une feuille de format A3 ; par réduction d’un facteur  (pourcentage approché de réduction 71 %), on passe de la même feuille de format A4 à une feuille de format A5 ;
(pourcentage approché de réduction 71 %), on passe de la même feuille de format A4 à une feuille de format A5 ; - une feuille de papier de format A0 contient deux feuilles A1, quatre feuilles A2, huit feuilles A3 et seize feuilles A4. Pour un papier de 80 g/m², une feuille A4, de dimensions approchée 21 cm × 29,7 cm, pèse donc cinq grammes. Bon à savoir lors de l’envoi d’un courrier postal…
Le format B possède les mêmes propriétés, mais la feuille de format B0 mesure 1 414 mm de longueur pour 1 000 mm de largeur. Les dimensions des feuilles de format C (format enveloppes) sont les moyennes géométriques des dimensions des feuilles correspondantes de format A et B.
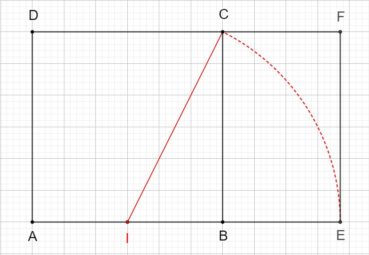
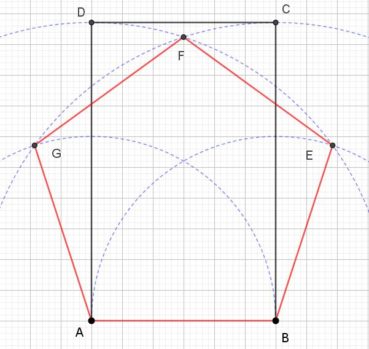
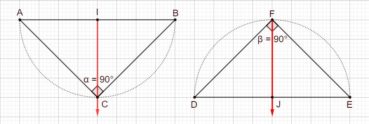
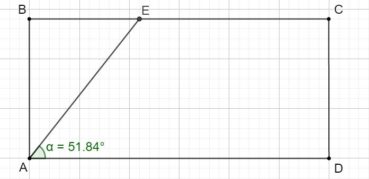
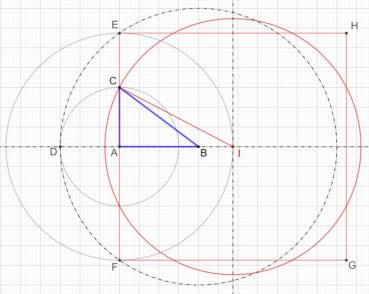
4.2. Le rectangle d’or et sa construction à la règle et au compas
Le rectangle d’or est un rectangle au format du nombre d’or : le rapport de sa longueur à sa largeur est égal à φ. La plus ancienne construction connue d’un rectangle d’or est celle d’Euclide (figure 4). Sa justification demande des connaissances en géométrie qui sont actuellement peu étudiées, et nous ne la donnerons pas.
La figure 5 donne une construction moderne, bien plus simple :
- ABCD est un carré de côté unité et I est le milieu de [AB],
- dans le triangle IBC, rectangle en B, le théorème de Pythagore donne
 ,
, - le cercle de centre I et de rayon IC coupe la demi-droite [AB) en E,
- les points A, I et E sont alignés, et IE = IC, donc
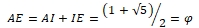 .
.
4.3. Propriétés du rectangle d’or
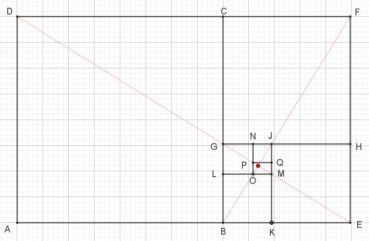
À la différence d’un rectangle au format A, qui se divise en deux rectangles de format A, un rectangle d’or ne se divise pas en deux rectangles d’or, mais en un carré et un rectangle d’or plus petit : on passe d’un rectangle d’or au suivant en divisant ses dimensions par ![]() .
.
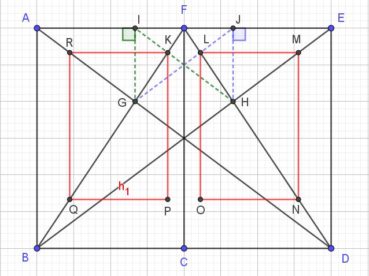
Sur la figure 6, le rectangle d’or AEFD est la réunion du carré ABCD et du rectangle d’or BEFC. De manière récursive, ce dernier contient à son tour le rectangle d’or BEHG, qui contient le rectangle d’or BKJG, qui contient le rectangle d’or LMJG, qui contient le rectangle d’or OMJN, qui contient le rectangle d’or OMQP, etc. Le point de convergence est le point rouge, intersection des segments [DE] et [BF]. Les points D, G, P, M, E sont alignés, de même que les points B, O, J, F.
5. Géométrie du pentagone
5.1. Pentagone régulier et nombre d’or
Avant le vie siècle av. J-C., les philosophes-mathématiciens grecs ne savaient construire, à la règle et au compas, que quelques polygones réguliers convexes, inscriptibles dans un cercle : triangle équilatéral, carré, hexagone et quelques autres comme l’octogone (à huit côtés) et le dodécagone (à douze côtés), qui s’en déduisent en construisant des bissectrices d’angles au centre.
Ils ont longtemps cherché, en vain, une méthode de trisection des angles (partage d’un angle en trois angles de même mesure) qui leur aurait permis de tracer facilement l’ennéagone régulier (à neuf côtés) en partant d’un triangle équilatéral : on sait maintenant que la trisection des angles est impossible à la règle non graduée et au compas. À cette époque, ils savaient aussi construire certains polyèdres convexes :
- tétraèdre, dont les quatre faces sont des triangles équilatéraux ;
- cube, dont les six faces sont des carrés ;
- octaèdre, dont les huit faces sont des triangles équilatéraux ;
- icosaèdre, dont les vingt faces sont des triangles équilatéraux et dans lequel, en groupant par cinq les faces ayant un sommet commun, on obtient des pyramides à base pentagonale.
Cependant, ne sachant pas construire le pentagone régulier, ils ne savaient pas encore construire le dodécaèdre, dont les douze faces sont des pentagones réguliers.
Ce sont les philosophes de l’école pythagoricienne qui, au vie siècle avant J.-C., ont trouvé la première construction du pentagone régulier à la règle et au compas. Cette construction est attribuée à Hippase de Métaponte, qui aurait découvert le lien entre le pentagone régulier et le nombre d’or, puis les premières propriétés connues de ce dernier.
Les connaissances de l’école pythagoricienne étaient réservées aux seuls initiés. Selon la tradition, Hippase de Métaponte aurait enfreint cette règle de confidentialité en divulguant ses découvertes. Pour cela, il aurait été exclu de l’école et un tombeau aurait été érigé à son nom pour que tout le monde sache qu’il était mort aux yeux de ses pairs. Selon d’autres sources, il se serait noyé, ou il aurait été noyé en mer par ses condisciples. La diffusion de certains secrets était impardonnable… Mais n’est-ce pas toujours le cas aujourd’hui ?
La construction du pentagone régulier a rendu possible celle du dodécaèdre régulier convexe (figure 147), dont les douze faces sont des pentagones réguliers. Tétraèdre, cube, octaèdre, dodécaèdre et icosaèdre sont les cinq « solides de Platon ».
Au cours des siècles, de nombreuses autres constructions et propriétés du pentagone régulier ont été découvertes (voir site Internet de P. Debart).
5.2. Pentagone régulier, pentagramme et pentacle
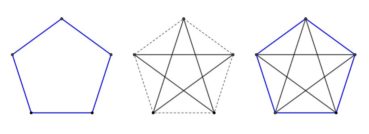
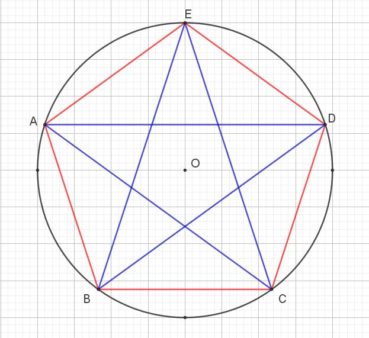
Un pentagone est un polygone plan à cinq côtés, convexe ou étoilé (figure 7).
Un domaine plan, délimité par une ligne fermée, est convexe lorsqu’il contient en entier tout segment reliant deux quelconques de ses points.
Un pentagone régulier est un pentagone convexe inscriptible dans un cercle, dont les cinq côtés sont de même longueur et les cinq angles au centre sont de même mesure 72° (ou ![]() radian).
radian).
Le pentagramme, ou pentagone étoilé ou encore étoile à cinq branches, est un pentagone non convexe obtenu en reliant, de deux en deux, les sommets d’un pentagone régulier.
Comme le triangle équilatéral et le carré, et à la différence de l’hexagone étoilé (formé de deux triangles équilatéraux imbriqués tête-bêche), le pentagramme peut se tracer sans lever le crayon. Les plus anciennes représentations connues (et approximatives) de pentagones étoilés ont été trouvées sur divers objets provenant d’antiques cités sumériennes, datés du ive millénaire av. J.-C. Dans l’Égypte ancienne, le hiéroglyphe représentant une étoile à cinq branches dans un cercle symbolisait le monde souterrain, lieu où disparaissent les étoiles à l’aube et dont elles ressortent au crépuscule, en une renaissance quotidienne et éternelle, alternée avec celle du soleil, et symbole du retour de la vie après la mort.
Le pentacle est un pentagone régulier, dans lequel on trace un pentagramme de mêmes sommets.
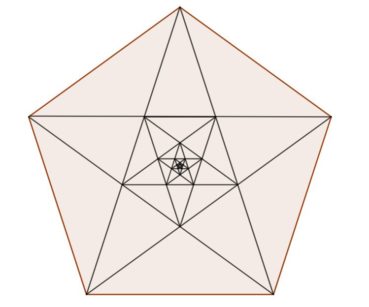
Les côtés du pentagramme forment au centre un petit pentagone régulier, dans lequel on peut de nouveau construire un pentagramme plus petit, et ainsi de suite jusqu’à l’infini (figure 146). Dans l’Antiquité, la suite de pentacles ainsi obtenus, rapidement trop petits pour être vus, symbolisait le mystère insondable de la création de l’univers. D’un point de vue mathématique, c’est probablement l’une des premières visualisations d’une suite infinie dont les termes convergent vers zéro.
5.3. Constructions du pentagone régulier à la règle et au compas
Nous ne donnerons pas ici la construction du pentagone régulier trouvée par l’école pythagoricienne, au vie siècle av. J.-C., car elle fait appel à des notions de géométrie actuellement peu familières (dont la « puissance d’un point par rapport à un cercle », inconnue des lycéens actuels). Les figures 8 et 9 donnent deux constructions simples plus récentes toutes deux liées au nombre d’or. D’autres constructions sont décrites sur le site Internet de P. Debart, donné en bibliographie.
Détail de la construction de la figure 8 :
- c est un cercle de centre O, [MN] et [PQ] sont deux diamètres perpendiculaires ;
- c’ est un cercle de diamètre[OP] et de centre O’, milieu de [OP] ;
- la demi-droite [MO’] coupe c’ en I et J ;
- le cercle c1 de centre M et de rayon [MJ] coupe c en A et en D. Le cercle c2 de centre M et de rayon [MI] coupe c en B et C.
Le polygone ABCDN est un pentagone régulier inscrit dans c. Prouvez-le !
Détail de la construction de la figure 9 :
- partant du rectangle d’or ABCD, tracer les cercles de centre A et de rayon [AB] et [AD], puis les cercles de centre B, et de rayon [BA] et [BC] ;
- ces cercles se recoupent E, F, G.
Le polygone ABEFG est un pentagone régulier. Prouvez-le !
5.4. Pentagone et pentagramme : construction, mesure des angles
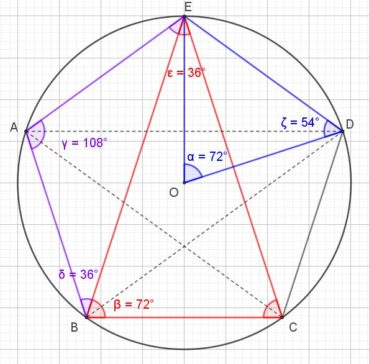
La figure 10 montre qu’un pentagramme se construit facilement en reliant, de deux en deux, les sommets d’un pentagone régulier.
La figure 11 donne les mesures des angles dans la figure précédente.
5.5. Les triangles d’or
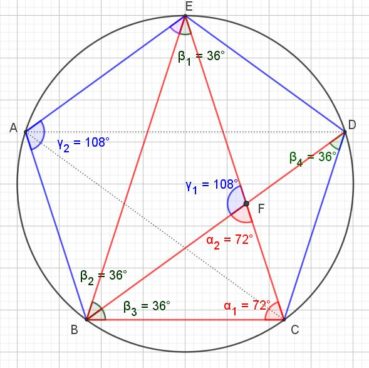
Sur la figure 12, on observe deux sortes de triangles d’or :
- les cinq triangles isométriques au triangle BCE sont des « triangles sublimes », ou « triangles d’Euclide »;
- les cinq triangles isométriques au triangle BCD sont des « triangles divins ».
Sur cette même figure, la diagonale [BD] est la bissectrice de l’angle ![]() . Elle coupe le segment [CE] en F, qui divise le segment [CE] en extrême et moyenne raison. Le triangle BCF est un triangle d’Euclide et le triangle CFD est un triangle divin.
. Elle coupe le segment [CE] en F, qui divise le segment [CE] en extrême et moyenne raison. Le triangle BCF est un triangle d’Euclide et le triangle CFD est un triangle divin.
Ceci montre comment construire récursivement une suite de triangles d’Euclide plus petits, sur le modèle du triangle BCF dans le triangle BCE, et une suite de triangles divins plus petits, sur le modèle du triangle CFD dans le triangle BCD.
5.6. Distances dans le pentagone, le pentagramme et les triangles d’or
Avec les notations de la figure 13 et en prenant comme unité de mesure la longueur de l’un des côtés du pentagone régulier ABCDE, on peut mesurer de nombreuses distances en fonction du nombre d’or . Entre autres :
- AB = BC = CD = DE = AE = 1 ;
- BC = BK = EK = 1 ;
- AC = AD = BD = BE = CE = φ ;
- CK = φ-1 ;
- CH = φ/2 = cos π/5 (π/5 radian = 36°).
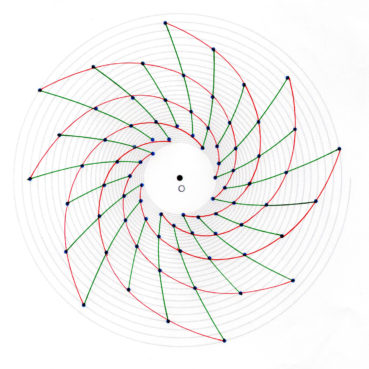
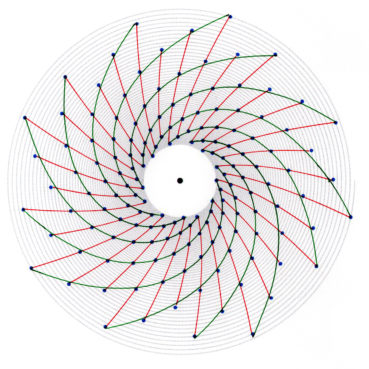
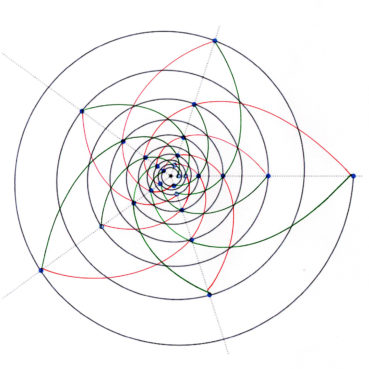
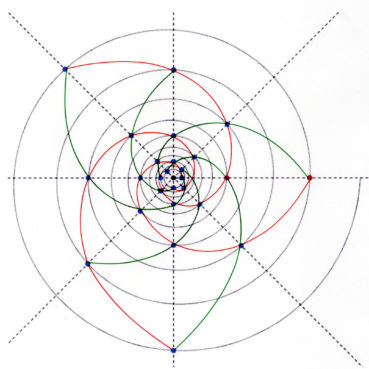
6. Nombre d’or et spirale
Les philosophes de l’école pythagoricienne ne connaissaient au plus que trois sortes de spirales : la spirale d’Archimède, la spirale du rectangle d’or, la spirale du triangle d’or.
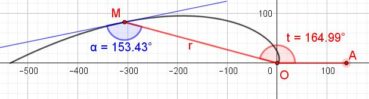
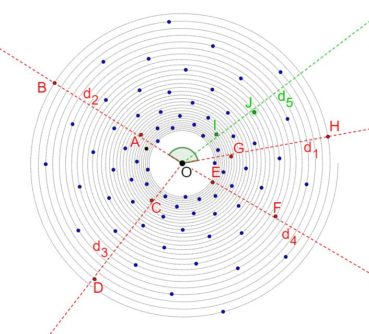
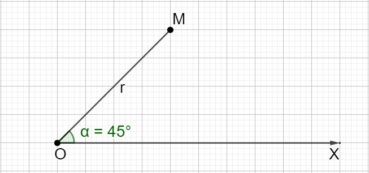
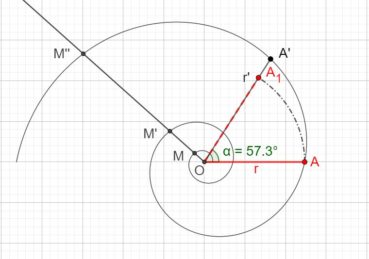
Sur chacune des spirales suivantes, le rayon vecteur est la longueur OM du segment [OM] ; la mesure de l’angle ![]() , normalement exprimée en radians, a été convertie en degrés. Voir dans le glossaire des compléments sur les notions développées dans ce paragraphe.
, normalement exprimée en radians, a été convertie en degrés. Voir dans le glossaire des compléments sur les notions développées dans ce paragraphe.
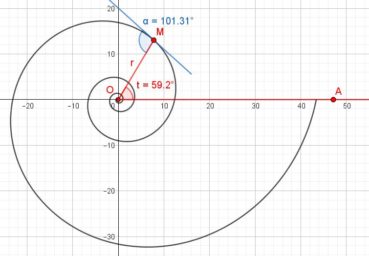
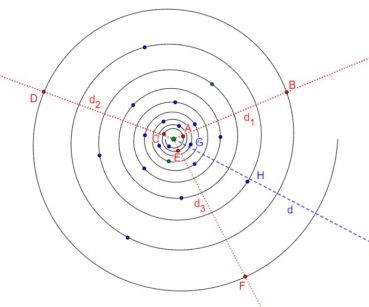
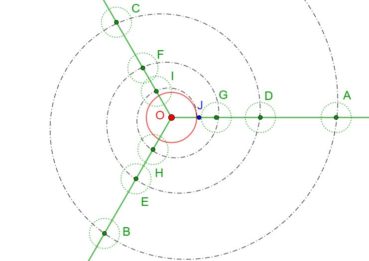
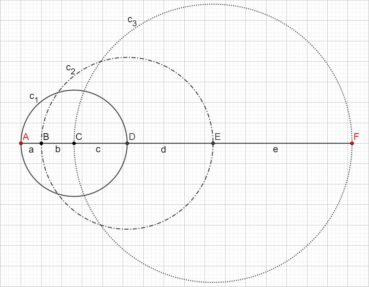
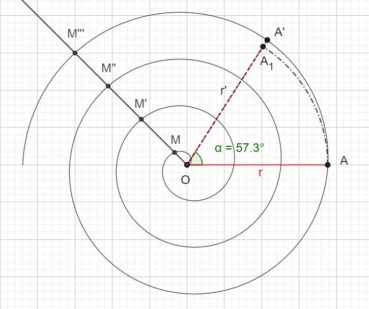
6.1. Spirale d’Archimède
Une spirale d’Archimède (figure 14) de centre O a une équation polaire de la forme ![]() , dans laquelle r est le rayon vecteur, α est l’angle et k est un nombre constant. L’écart radial entre deux spires est constant. Une spirale d’Archimède peut être visualisée en enroulant une corde sur une surface plane.
, dans laquelle r est le rayon vecteur, α est l’angle et k est un nombre constant. L’écart radial entre deux spires est constant. Une spirale d’Archimède peut être visualisée en enroulant une corde sur une surface plane.
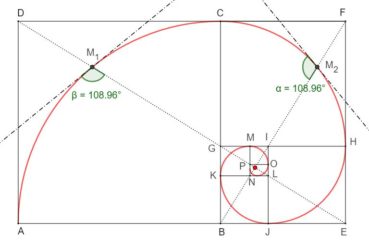
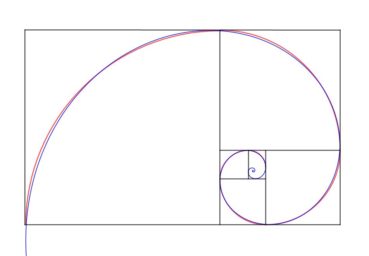
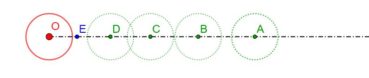
6.2. Spirale du rectangle d’or
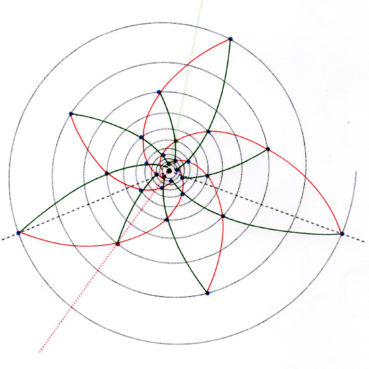
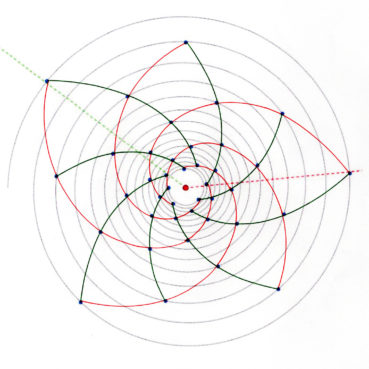
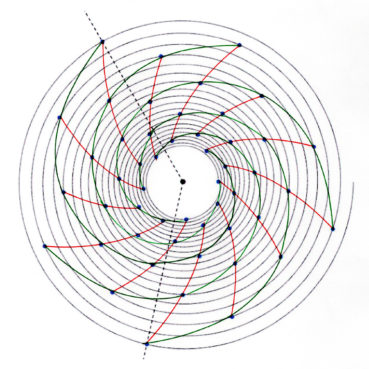
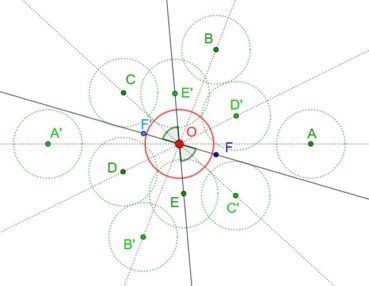
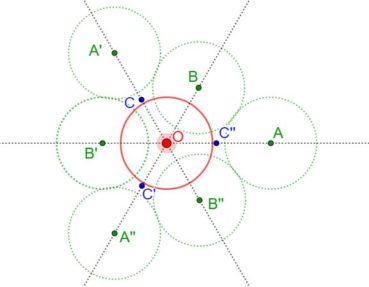
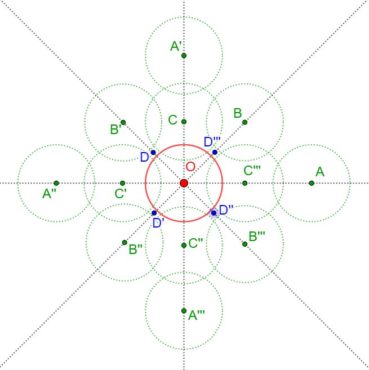
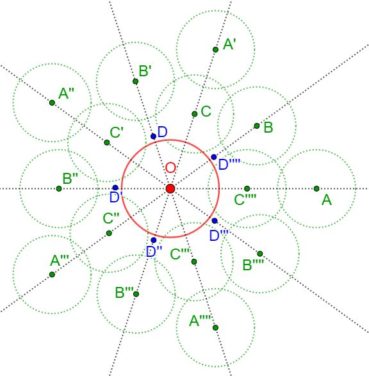
La spirale du rectangle d’or (figure 15) de centre Ω (point rouge à l’intersection des segments [DE] et [BF]) est la réunion de quarts de cercles de centres successifs B, G, I, L, N, P, etc. La spirale du rectangle d’or est unique, à un changement d’échelle près. L’angle que fait le segment [ΩM1] avec la tangente en M1 à la courbe a pour mesure constante 108,96°.
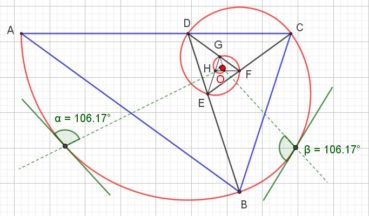
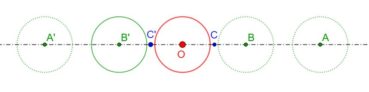
6.3. Spirale du triangle d’or
La spirale du triangle d’or (figure 16), de centre O, est la réunion d’arcs de cercles de centres successifs D, E, F, G, H, etc. La spirale du triangle d’or est unique, à un changement d’échelle près. L’angle que fait le segment [OM] avec la tangente en M à la courbe a pour mesure constante 106,17°.
6.4. Spirales exponentielles (ou spirales logarithmiques)
Une spirale exponentielle (figures 17 et 18) a pour équation polaire ![]() . Dans cette équation, r est la distance OM, qui varie de manière continue en fonction de la mesure de l’angle
. Dans cette équation, r est la distance OM, qui varie de manière continue en fonction de la mesure de l’angle ![]() ; a est un coefficient de dilatation qui permet un ajustement d’échelle ; b détermine la vitesse avec laquelle le point M s’éloigne du centre O de la spirale, donc la mesure de l’angle α que fait le segment [OM] avec la tangente en M à la courbe.
; a est un coefficient de dilatation qui permet un ajustement d’échelle ; b détermine la vitesse avec laquelle le point M s’éloigne du centre O de la spirale, donc la mesure de l’angle α que fait le segment [OM] avec la tangente en M à la courbe.
Les spirales exponentielles partagent une propriété exclusive : lorsque la valeur de la variable t augmente, la surface enfermée entre leurs spires se dilate de manière autosimilaire, en conservant ses proportions initiales.
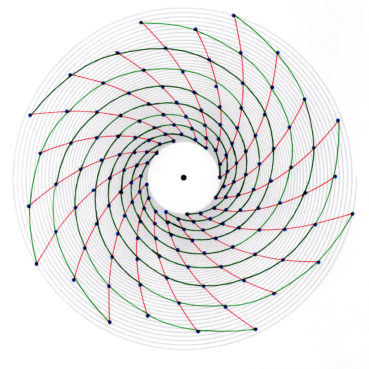
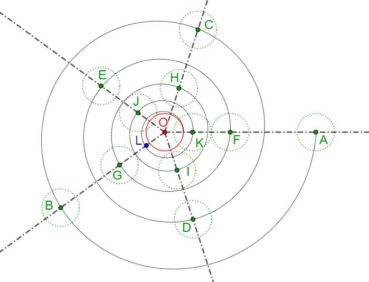
6.5. La spirale du rectangle d’or est-elle une spirale exponentielle ?
La spirale du rectangle d’or est souvent confondue avec une spirale exponentielle. Bien qu’elle soit une bonne approximation d’une spirale exponentielle bien précise (figure 19), elle diffère des spirales exponentielles par les points suivants :
- La spirale du nombre d’or est unique, à un changement d’échelle près, alors qu’une spirale exponentielle peut avoir différentes formes, dépendant en premier du choix du paramètre b, qui détermine la valeur de r en fonction de celle de t, puis du choix du paramètre a, coefficient de dilatation qui permet un ajustement d’échelle.
- Comme toute spirale exponentielle, la spirale du rectangle d’or de centre O est équiangle : l’angle que fait [OM] avec la tangente en M à la courbe est constant. Pour la spirale du rectangle d’or, cet angle est toujours égal à 108,96° (figure 15) alors que, pour chaque spirale exponentielle, cet angle est fixé par la valeur donnée au paramètre b (figures 17 et 18).
- Le rayon de courbure d’une courbe est le rayon du cercle tangent qui approche au mieux cette courbe au point de contact.
- pour la spirale du rectangle d’or, le rayon de courbure est constant par intervalles et il varie par sauts successifs : avec les notations de la figure 15, si le rayon de courbure de l’arc (AC) est égal à 1/φ, alors que celui de l’arc (CH) est égal à 1/, celui de l’arc suivant est égal à 1/φ2, etc. ;
- pour toute spirale exponentielle, le rayon de courbure varie de manière continue en fonction de la valeur de t.
Ces deux types de spirales sont donc bien différents, même si la première est visuellement bien approchée par la spirale exponentielle de paramètre ![]() , de valeur décimale approchée 0,30635 (Rousseau & Zazoun, 2008, Spirales végétales). La figure 19 permet de visualiser la bonne qualité de cette approximation.
, de valeur décimale approchée 0,30635 (Rousseau & Zazoun, 2008, Spirales végétales). La figure 19 permet de visualiser la bonne qualité de cette approximation.
Pour réaliser cette figure, commencer par construire un rectangle d’or tel que le centre de la spirale du rectangle d’or qu’il contient soit confondu avec le centre O du repère dans lequel on trace ensuite la spirale exponentielle.
6.6. Spirales exponentielles dans la nature
Des spirales exponentielles – courbes délimitant des aires dans le plan, surfaces délimitant des solides dans l’espace – s’observent chez de nombreux êtres vivants : elles donnent leur forme aux cornes des bouquetins (figure 20), des mouflons, des antilopes, aux défenses des éléphants (et celles, fossiles, des mammouths), aux coquilles des gastéropodes terrestres ou marins, actuels ou fossiles (figure 21), etc.
Dès le début de leur croissance, ces cornes, défenses ou coquilles sont contraintes par leurs parties rigides déjà formées, qui ne peuvent plus être modifiées : la croissance ne peut se continuer à l’identique qu’en adoptant une forme de cône (droit) ou de spirale exponentielle enroulée à plat (nautiles actuels, ammonites fossiles) ou en hélice conique plus ou moins aplatie ou allongée. Le corps mou d’un gastéropode, abrité par sa coquille, peut ainsi grandir sans modification de ses proportions initiales.
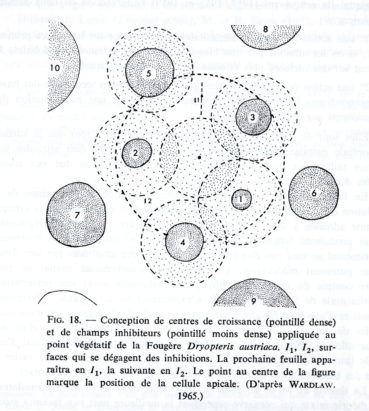
Chez des végétaux, des spirales exponentielles s’observent sur les jeunes frondes de fougères en début de croissance (figure 22), mais aussi (pages 61 à 65) sur les capitules des Asteracées, les structures fractales du chou romanesco, les ombelles des carottes, les cônes des conifères, les plantes succulentes des déserts, etc.
Des spirales exponentielles s’observent aussi dans des phénomènes naturels de grande dimension : enroulement des nuages dans les cyclones, bras des galaxies spirales.
7. Nombre d’or et suite de Fibonacci
7.1. La suite de Fibonacci
La suite de Fibonacci est célèbre pour la façon dont elle a été définie par Léonardo Fibonacci, dans son ouvrage Liber abaci, publié en 1202, mais elle était connue bien avant cette publication (pages 80 à 83).
Voici, en langage actuel, une définition de cette suite, inspirée de celle donnée par Fibonacci : « un couple de lapins juvéniles, enfermé dans un enclos dans lequel il a de quoi se nourrir ainsi que sa descendance, devient fertile au bout d’un mois, puis donne naissance à un nouveau couple de lapins à la fin de chaque mois suivant. Chaque nouveau couple fait de même. Combien de couples pourra-t-on compter à la fin de l’année ? ». Dans ce processus assez peu réaliste, on suppose que chaque nouveau couple est formé d’un mâle et d’une femelle, que tous les lapins sont fertiles et restent en vie, et on ne s’occupe pas de la consanguinité… On note x un couple juvénile, X ce même couple devenu fertile et X ce même couple avec descendance. Le nombre des couples successivement obtenus après chaque étape est noté u0, u1, u2, u3, u4 … et plus généralement un. Initialement, il y a un seul couple, le couple juvénile a : u0 = 1
Au bout de 1 mois, le couple a est devenu fertile, mais encore sans descendance. La population est composée de A seul : u1 = 1.
Au bout de 2 mois, du couple A naît un couple juvénile b. La population est composée des couples A, b : u2 = 2.
Au bout de 3 mois, du couple A naît à un nouveau couple juvénile c, et le couple b devient fertile. La population est composée des couples A, B, c : u3 = 3
Au bout de 4 mois, du couple A naît un nouveau couple juvénile d, du couple B naît un couple juvénile e et le couple c devient fertile. La population est composée des couples A, B, C, d, e : u4 = 5.
Au bout de 5 mois, chacun des couples A, B et C donne naissance à un couple juvénile (respectivement f, g, h) et les couples d et e deviennent fertiles. La population est composée des couples A, B, C, D, E, f, g, h : u5 = 8.
Le processus continue : il apparaît que chaque terme d’indice supérieur à 2 est la somme des deux termes précédents, ce qui définit une suite additive (plus précisément une suite récurrente linéaire d’ordre 2) telle que
u0 = u1 = 1 puis un+2 = un+1 + un.
Lorsqu’elle n’illustre pas le processus fantaisiste décrit par Fibonacci, la suite peut être définie par les premiers termes u0 = 0 et u1 = 1 . Les valeurs successives de un deviennent 0, 1, 1, 2, 3, 5, 8, etc., avec un simple décalage d’indice par rapport à la définition initiale donnée par Fibonacci.
Dans ce qui suit, la relation un+2 = un+1 + un est appelée « algorithme de Fibonacci ».
En mathématiques, la suite de Fibonacci et d’autres suites récurrentes linéaires d’ordre 2 interviennent dans les équations diophantiennes (équations de la forme ax + by = c , avec a, b et c entiers, dont on cherche des solutions entières pour les inconnues et ) et dans divers problèmes de dénombrement. En biologie, on rencontre la suite de Fibonacci en botanique (voir pages 20 à 26). Elle apparaît aussi lorsqu’on étudie la généalogie dans les populations de certains insectes, comme les abeilles, dont la reproduction est alternativement sexuée ou parthénogénétique : les œufs fécondés donnent des femelles (qui seront le plus souvent des ouvrières) et les œufs non fécondés donnent des mâles.
7.2. Liens entre la suite de Fibonacci et le nombre d’or
En mathématiques, la suite de Fibonacci est la plus simple des suites récurrentes linéaires d’ordre 2, définies par une relation du type ![]() , dans laquelle a et b sont des valeurs numériques constantes et les deux premiers termes u0 et u1 sont donnés. La relation
, dans laquelle a et b sont des valeurs numériques constantes et les deux premiers termes u0 et u1 sont donnés. La relation ![]() peut aussi s’écrire
peut aussi s’écrire ![]() .
.
On lui associe le polynôme caractéristique x2 – ax – b, puis l’équation caractéristique x2 – ax – b = 0. L’équation caractéristique associée à la suite de Fibonacci est x2 – x – 1 = 0. En page 4, nous avons vu que les racines de cette équation sont φ et 1 – φ. En page 6, nous avons déduit de la relation φ2 – φ – 1 = 0 le développement de φ en fraction continue :
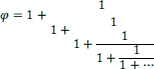
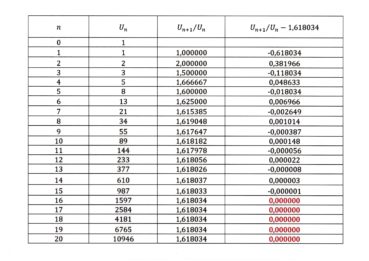
En page 8, nous avons vu que le calcul des réduites successives de cette fraction continue donne des valeurs approchées de plus en plus précises du nombre φ, que nous noterons ![]() . Voici les calculs des premières réduites de φ, les pointillés désignant les parties fractionnaires non encore prises en compte :
. Voici les calculs des premières réduites de φ, les pointillés désignant les parties fractionnaires non encore prises en compte :
![]()
![]()
![]()
Successivement :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
, etc.
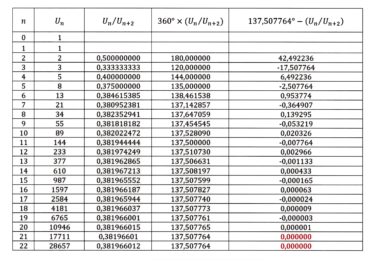
On reconnaît dans ces termes le quotient ![]() de deux termes consécutifs de la suite de Fibonacci. Le tableau 1 permet de comparer, lorsque augmente, la valeur de ce quotient
de deux termes consécutifs de la suite de Fibonacci. Le tableau 1 permet de comparer, lorsque augmente, la valeur de ce quotient ![]() avec celle du nombre d’or, de valeur approchée 1,618034.
avec celle du nombre d’or, de valeur approchée 1,618034.
On peut conjecturer que, lorsque tend vers plus l’infini, la limite du quotient ![]() est égale à φ. La convergence est rapide et la limite est alternativement approchée par valeurs inférieures et par valeurs supérieures. Ce résultat surprenant a été démontré par Kepler en 1608. En voici une preuve.
est égale à φ. La convergence est rapide et la limite est alternativement approchée par valeurs inférieures et par valeurs supérieures. Ce résultat surprenant a été démontré par Kepler en 1608. En voici une preuve.
Soit L la limite, lorsque n tend vers l’infini, du quotient ![]() . C’est aussi la limite du quotient
. C’est aussi la limite du quotient ![]() .
.
![]()
![]()
![]()
![]()
![]()
Cette équation s’écrit L2 – L – 1 = 0. Nous avons vu (page 4) qu’elle définit le nombre d’or, ce qui prouve que L = φ .
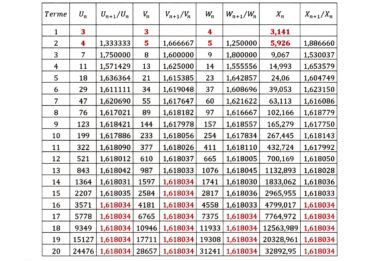
Une remarque importante s’impose : cette démonstration ne demande pas que la suite considérée soit exactement la suite de Fibonacci, mais seulement qu’elle soit définie par l’algorithme de Fibonacci, indépendamment de la valeur de ses deux premiers termes (tableau 2).
Vous pouvez refaire un tableau comparable en donnant des valeurs quelconques aux deux premiers termes, sous réserve que ces valeurs soient toutes deux positives, afin d’éviter une division par zéro au cours des calculs.
Dans le tableau 2, la suite ![]() a pour premiers termes deux nombres consécutifs de la suite de Fibonacci : le quotient
a pour premiers termes deux nombres consécutifs de la suite de Fibonacci : le quotient ![]() converge vers φ plus rapidement que les autres quotients comparables. Avez-vous reconnu les nombres x1 et x2 ? Ils ont été formés à partir des premiers chiffres significatifs du développement décimal de π …, illustration du fait que les deux premiers termes peuvent être quelconques.
converge vers φ plus rapidement que les autres quotients comparables. Avez-vous reconnu les nombres x1 et x2 ? Ils ont été formés à partir des premiers chiffres significatifs du développement décimal de π …, illustration du fait que les deux premiers termes peuvent être quelconques.
Nous verrons plus loin (pages 80 à 83) que cette propriété explique que les bâtisseurs du Moyen Âge n’avaient pas à connaître et à utiliser (de manière cryptée) le nombre d’or pour que celui-ci apparaisse dans les proportions des cathédrales.
7.3. Autres liens entre la suite de Fibonacci et le nombre d’or
Parmi les nombreuses propriétés liant la suite de Fibonacci et le nombre d’or, étudions la suite géométrique de premier terme et de raison , donc de second terme . Sachant que , les termes successifs de cette suite sont :
b = a x φ
c = b x φ = a x φ² = a x (1+φ) = a + a x φ = a + b
d = c x φ = a x (φ + φ²) = a x (φ + (1 + φ)) = a x (1 + 2φ) = b + c = a + 2b
Selon le même processus, et de proche en proche, en jonglant sur les propriétés de φ :
e = d x φ = a x φ4 = … = a x (2 + 3φ) = c + d = 2a + 3b
f= e x φ = a x φ5 = … = a x (3 + 5φ) = d+ e = 3a + 5b
g= f x φ = a x φ6 = … = a x (5 + 8φ) = e + f = 5a + 8b
h= g x φ = a x φ7 = … = a x (8 + 13φ) = f + g = 8a + 13b
i= h x φ = a x φ8 = … = a x (13 + 21φ) = g + h = 13a + 21b
j= i x φ = a x φ9 = … = a x (21 + 34φ) = h + i = 21a + 34b
k= j x φ = a x φ10 = … = a x (34 + 55φ) = i + j = 34a + 55b
l= k x φ = a x φ11 = … = a x (55 + 89φ) = j + k = 55a + 89b
m= l x φ = a x φ12 = … = a x (89 + 144φ) = k + l = 89a + 144b
n= m x φ = a x φ13 = … = a x (144 + 233φ) = l + m = 144a + 233b
et ainsi de suite pour les termes suivants.
Les nombres a, b, c, d, e, f se calculent à la fois, de proche en proche, en tant que :
- termes consécutifs d’une suite géométrique de premier terme
 et de raison φ telle que
et de raison φ telle que 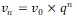 ;
; - termes d’une suite linéaire récurrente d’ordre 2, de terme général
 définie par la même relation récurrente que la suite de Fibonacci et reliée à cette dernière par les relations
définie par la même relation récurrente que la suite de Fibonacci et reliée à cette dernière par les relations  , dans lesquelles un et un+1 sont les termes d’indices correspondants de la suite de Fibonacci.
, dans lesquelles un et un+1 sont les termes d’indices correspondants de la suite de Fibonacci.
7.4. Liens entre la suite de Fibonacci et l’angle d’or
Nous avons vu (page 6) que l’angle d’or α a pour mesure ![]() radians et que sa mesure en degrés est égale à
radians et que sa mesure en degrés est égale à ![]() , de valeur approchée usuelle 137,5°. Dans la suite de Fibonacci :
, de valeur approchée usuelle 137,5°. Dans la suite de Fibonacci : ![]() et
et ![]() , d’où
, d’où ![]() . Lorsque n tend vers l’infini, la limite de
. Lorsque n tend vers l’infini, la limite de ![]() est égale à la mesure en degrés de l’angle d’or, cette limite étant alternativement approchée par excès et par défaut.
est égale à la mesure en degrés de l’angle d’or, cette limite étant alternativement approchée par excès et par défaut.
Le tableau 3 permet de visualiser la vitesse de la convergence. Pour gagner en précision, les calculs ont été faits en prenant la valeur 137, comme mesure approchée de l’angle d’or.
Le rapport ![]() sera associé aux indices de phyllotaxie (page 21) et ainsi lié à l’angle d’or et au nombre d’or. Nous verrons que les premières valeurs de
sera associé aux indices de phyllotaxie (page 21) et ainsi lié à l’angle d’or et au nombre d’or. Nous verrons que les premières valeurs de ![]() , pour lesquelles un+2 est un diviseur de 360, sont associées à des indices de phyllotaxie particuliers et à des angles de divergence respectifs de 360°, 180°, 120°, 144° et 135°.
, pour lesquelles un+2 est un diviseur de 360, sont associées à des indices de phyllotaxie particuliers et à des angles de divergence respectifs de 360°, 180°, 120°, 144° et 135°.
PARTIE II
Angle d’or et suite de Fibonacci en botanique
Deux observations préalables – Observons deux plantes dont les feuilles sont alternes (chaque nœud de la tige ne porte qu’une seule feuille) et disposées en spirale (plus précisément en hélice) autour de la tige, disposition qui se retrouve chez de nombreuses espèces de plantes. Les figures 23 et 24 illustrent Phytolacca americana, une Dicotylédone nord-américaine photographiée dans le jardin de l’auteur ; la figure 25 illustre Aloe perfoliata, une Monocotylédone originaire des zones désertiques ou semi-désertiques d’Afrique du Sud, photographiée dans les serres du Conservatoire botanique Pierre-Fabre.
Recherchons, pour le spécimen de la figure 24, une valeur moyenne de l’angle de divergence entre les pétioles de deux feuilles consécutives, mesuré perpendiculairement à l’axe de la tige. Pour cela, les feuilles de la tige principale – développées avant formation des trois jeunes rameaux portant de plus petites feuilles – ont été numérotées de 1, pour la plus récente, à 12, pour la plus ancienne. La feuille 11, cachée par la feuille 6, n’a pas pu être prise en compte, de même que les suivantes (seule la feuille 12 est visible). Un trait blanc indique, aussi précisément que possible, la direction de la base du pétiole de chacune de ces feuilles, ce qui permet de mesurer approximativement neuf angles de divergence (avec une précision toute relative : la tige n’étant pas parfaitement rectiligne, les axes ne convergeaient pas tous en un seul point). À un ou deux degrés près, ces angles ont des mesures comprises entre 122° et 146°, avec une valeur moyenne de 138,7°. La différence avec la mesure de l’angle d’or, de valeur approchée 137,5°, n’est que de 1,2°.
Pour Aloe perfoliata, la procédure est la même que ci-dessus, après matérialisation des axes des feuilles par un trait rouge. Sur ce spécimen, le haut de la tige était presque rectiligne : sur la photographie, les traits rouges convergent en un seul point et quinze feuilles ont pu être numérotées. Leurs angles de divergence peuvent être mesurés avec une assez bonne précision et leurs mesures sont comprises entre 121° et 151°. Leur valeur moyenne arrondie est égale à 137,6°. Elle ne diffère de celle de l’angle d’or que de 0,1°.
Est-ce une simple coïncidence si, dans chacun des deux exemples précédents, les mesures des angles moyens de divergence sont à la fois si proches entre elles et si proches de la mesure de l’angle d’or ? Ce qui suit nous montrera que non et nous fera peut-être découvrir bien d’autres propriétés, à la fois botaniques et mathématiques.
8. La phyllotaxie
La phyllotaxie est la science qui « décrit la disposition des feuilles les unes par rapport aux autres sur la tige d’un végétal » (Jouy & de Foucault, 2016).
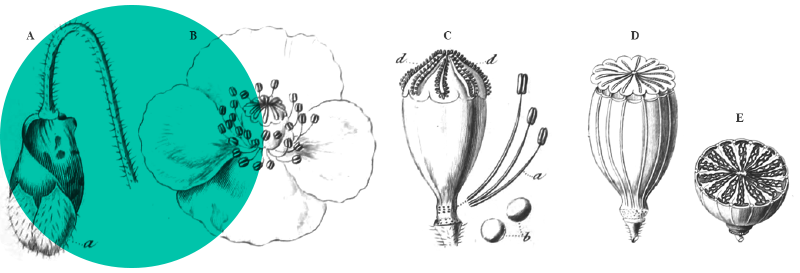
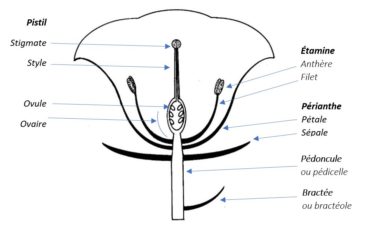
L’exemple d’une branche de Ficus carica (figure 26) nous permettra de décrire les différentes parties d’un jeune rameau de cette plante et le vocabulaire qui lui est associé :
- 1 : limbe d’une feuille ;
- 2 : pétiole de cette feuille ;
- 3 : nœuds, soulignés par les traces laissées par les stipules ;
- 3 : entrenœud ;
- 5 : bourgeons axillaires ;
- 6 : apex de la tige en croissance, dont le méristème est abrité par les stipules des feuilles en formation ;
- 7 : stipules caduques protégeant une jeune feuille en formation (qui peut ne pas se développer, mais le bourgeon axillaire subsiste) ;
- 8 : extrémité du rameau de l’année précédente ;
- 9 : figue d’été, aussi appelée « figue fleur », issue d’un bourgeon proche de l’extrémité du rameau de l’année précédente. Les figues d’automne seront issues de bourgeons axillaires naissant à l’aisselle des pétioles des jeunes feuilles de l’année.
La disposition des feuilles d’une plante se retrouve évidemment sur les bourgeons et les rameaux qui naissent à l’aisselle de leurs pétioles, mais aussi sur les inflorescences portant des fleurs en grappe, en corymbe, en capitule, en ombelle, etc. (figure 153).
Les écailles des cônes des Conifères et les pièces florales des fleurs des Angiospermes sont interprétées comme d’anciennes feuilles qui, au cours de l’évolution, se sont modifiées pour permettre la reproduction sexuée telle que nous l’observons actuellement. En conséquence, on devrait retrouver la disposition des aiguilles d’un cône de Conifère sur les écailles de ce cône et la disposition des feuilles d’une Angiosperme sur les pièces florales de ses fleurs. Mais ce n’est pas toujours évident lorsqu’on les observe, car l’évolution des feuilles en écailles ou en pièces florales – qui sont habituellement peu nombreuses et qui se développent sur un axe très court – s’est faite avec de multiples modifications et simplifications. Lorsqu’elles sont suffisamment nombreuses, les écailles d’un cône sont visiblement réparties le long d’une hélice et elles forment des parastiches, alors que, chez une grande majorité des plantes à fleurs, les pièces florales sont groupées par niveaux successifs superposés, appelés verticilles (les figures 32 et 33 illustrent des exceptions).
9. Caractérisation de la phyllotaxie par un indice
9.1. L’indice de phyllotaxie
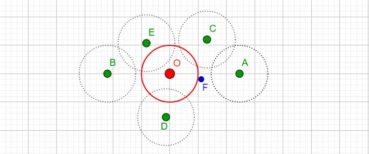
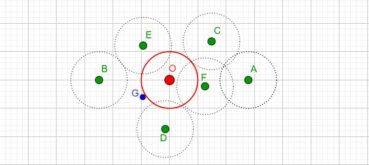
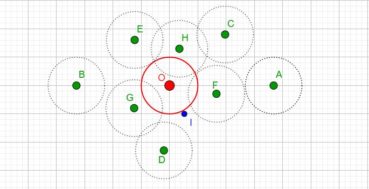
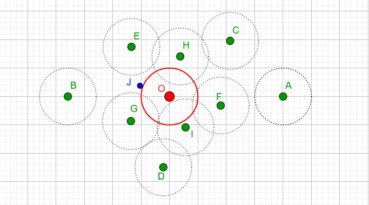
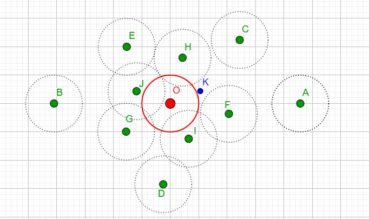
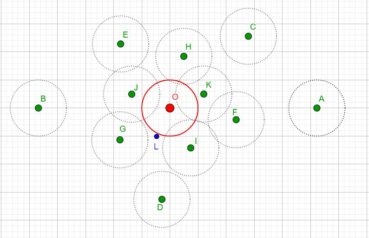
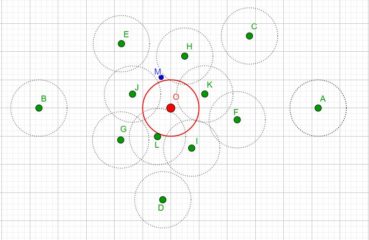
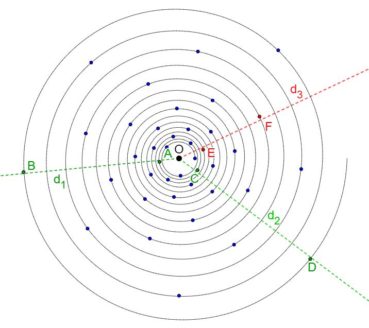
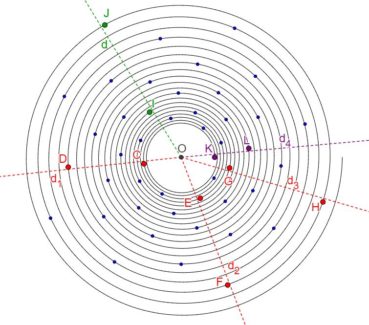
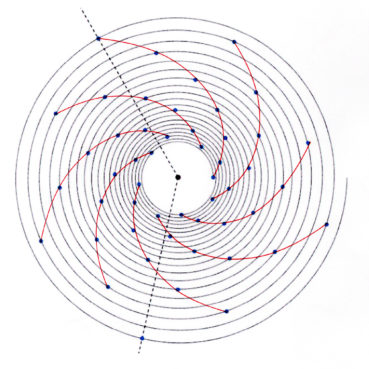
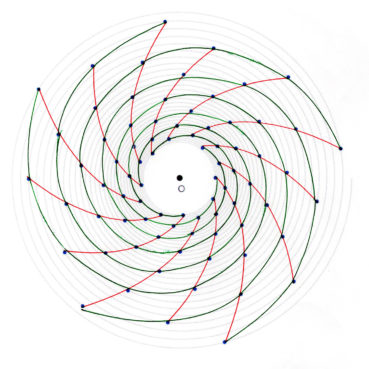
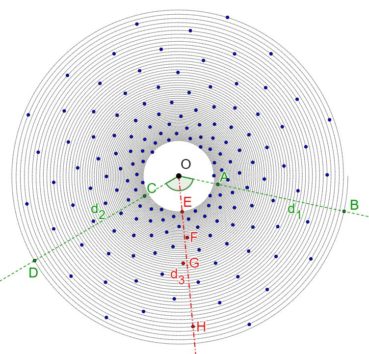
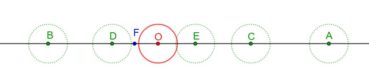
Jusqu’à la fin du xxe siècle, les différentes phyllotaxies ont été caractérisées par des indices de phyllotaxie. Sur un spécimen donné, on repère deux feuilles dont les pétioles occupent, avec la meilleure approximation possible, la même position sur la tige : vues dans l’axe de cette dernière, supposée non vrillée, les feuilles sont approximativement superposées. On compte alors le nombre A de spires qui séparent la première feuille de la seconde, puis le nombre B d’entrenœuds entre la première et la seconde. L’indice de phyllotaxie est le rapport A/B.
Pour faciliter le décompte, on peut entourer une cordelette autour de la tige, en la faisant passer sous la base de chaque pétiole (figure 28). Si par exemple les feuilles occupant approximativement une même position sur la tige sont séparées par trois spires et huit entrenœuds, alors l’indice de phyllotaxie est égal à 3/8 puisque A = 3 et B = 8.
Les indices de phyllotaxie les plus fréquemment observés sont, par ordre simultanément croissant de leurs numérateurs et dénominateurs :
1/1 ; 1/2 ; 1/3 ; 2/5 ; 3/8 ; 5/13 ; 8/21 ; 13/34; etc.
Les angles de divergence moyens associés à ces indices ont pour mesures respectives :
360° ; 180° ; 120° ; 144° ; 135° ; 138,46° ; 137,14° ; 137,65° ; etc.
Les botanistes ont remarqué depuis longtemps que, sauf pour le premier, les indices de phyllotaxie sont de la forme un/un+2, où un+2 et sont des termes de la suite de Fibonacci. Nous savons (tableau 3) que, lorsque n augmente, les angles de divergence associés se rapprochent progressivement de l’angle d’or, alternativement par valeurs supérieures et par valeurs inférieures.
9.2. Quelques exemples
Quels indices de phyllotaxie pouvons-nous attribuer au Raisin d’Amérique et à l’Aloé perfolié ? Pour le spécimen de Raisin d’Amérique (figures 23 et 24), la meilleure superposition de feuilles est obtenue pour les feuilles 6 et 11 ; on dénombre cinq entrenœuds pour deux spires : l’indice de phyllotaxie est égal à 2/5. Pour le spécimen d’Aloé perfolié (figure 25), la meilleure superposition de feuilles est obtenue pour les feuilles 3 et 11 ; on dénombre huit entrenœuds pour trois spires : l’indice de phyllotaxie est égal à 3/8. Dans ces deux cas, l’écart entre l’angle d’or et l’angle de divergence est moindre lorsqu’on fait une observation directe que lorsqu’on considère l’angle théorique associé à l’indice de phyllotaxie.
Considérons maintenant un même rejet d’Arbousier, photographié dans le jardin de l’auteur. La figure 27 montre le rejet fin 2018 et la figure 28 montre la jeune pousse qui l’a prolongé au cours du printemps 2019. Ces deux observations montrent que, sur un même spécimen, l’indice de phyllotaxie peut varier d’une année à l’autre, qu’il dépend de l’appréciation d’un alignement (lequel n’est a priori jamais parfait) et, au moins sur l’exemple étudié, du stade de développement et de la vigueur de la pousse considérée.
Sur la figure 27, les pétioles des feuilles numérotées 0 et 8 sont approximativement alignés ; on compte huit entrenœuds pour trois spires, on peut attribuer au rejet un indice de phyllotaxie égal à 3/8. Sur la figure 28, les pétioles des feuilles numérotées 0 et 13 sont approximativement alignés ; on compte treize entrenœuds pour cinq spires (un fil rouge a été enroulé autour de la tige, à la base des pétioles, pour matérialiser ces spires), on peut maintenant attribuer au rejet un indice de phyllotaxie égal à 5/13.
Est-il exceptionnel de pouvoir donner deux indices de phyllotaxie différents à un même spécimen ? Non, nous en verrons d’autres exemples plus loin. C’est pourquoi une autre approche, présentée dans les pages suivantes, est actuellement privilégiée.
10. Caractérisation de la phyllotaxie par le nombre de feuilles par nœud et par l’angle de divergence
Les différentes phyllotaxies sont actuellement décrites et classées en fonction du nombre de feuilles par nœud et de l’angle de divergence entre feuilles consécutives, ou groupées sur un même nœud. Cette caractérisation simplifie et harmonise la notion d’indice de phyllotaxie.
10.1. Phyllotaxies alternes : une seule feuille par nœud
Les feuilles sont alternes, les entrenœuds sont régulièrement espacés.
10.1.1 Phyllotaxie alterne spiralée standard : l’angle moyen de divergence est l’angle d’or, de mesure approchée 137,5°
Les feuilles sur la tige ou les fleurs dans une inflorescence s’enroulent en hélice autour de la tige. Elles ne forment pas d’orthostiches (alignements radiaux) mais peuvent former des parastiches (alignements sur des spirales ou des hélices) lorsqu’elles sont nombreuses et serrées. Cette phyllotaxie, majoritaire chez les plantes à fleurs, est illustrée par la figure 29 et modélisée sur les figures 75_1 à 75_13. La figure 30 illustre la phyllotaxie alterne spiralée standard des inflorescences en grappes ; des parastiches sont visibles sur les fleurs non écloses.
Attention aux apparences ! La figure 31 illustre la phyllotaxie alterne spiralée standard du Sapin pectiné (Abies alba). Les aiguilles portées par les jeunes rameaux ont des limbes disposés en double peigne, mais leurs pétioles sont insérés en hélice, puis vrillés à leur base, optimisant l’exposition de chaque limbe à la lumière. Chez Abies nordmanniana, les limbes sont disposés en brosse unilatérale ; chez Abies pinsapo, ils sont entièrement disposés en écouvillons spiralés, comme leurs pétioles.
Au lieu d’être toutes disposées en verticilles superposés, comme chez la plupart des autres plantes à fleurs, les pièces florales de certaines Magnoliacées et Ranunculacées ont conservé un caractère ancestral : leur phyllotaxie est alterne spiralée standard. Au moins les étamines et les carpelles d’Adonis annua et de Ranunculus kuepferi (figure 32), et de Ranunculus aconitifolius (figure 33, à gauche) sont disposés sur un réceptacle plus ou moins conique ou en pain de sucre. Noter les parastiches, bien visibles sur les étamines de Ranunculus aconitifolius. De nombreuses Ranunculacées ont des pétales (ou des tépales) en nombre variable et plus ou moins visiblement disposés sur une hélice à pas très court, comme les pales d’une turbine : le bord de chaque pétale recouvre partiellement le pétale suivant. La plupart des autres renoncules ont des fleurs à cinq pétales verticillés, dont les bords ne se chevauchent pas.
Toutes les pièces florales de Magnolia grandiflora (figure 33, à droite) sont disposées en hélices serrées sur le haut du pédicelle.
10.1.2 Autres phyllotaxies alternes spiralées : l’angle moyen de divergence n’est pas l’angle d’or
Les feuilles s’enroulent en hélice autour de la tige en formant un ou plusieurs alignements radiaux, appelés orthostiches.
10.1.2a Phyllotaxie alterne monostique
Les feuilles se répartissent unilatéralement sur une seule orthostiche (figure 34). L’angle de divergence mesure en moyenne 360°. Cette phyllotaxie, rarement observée, est modélisée sur la figure 89.
10.1.2b Phyllotaxie alterne distique
Les feuilles se répartissent, de part et d’autre de la tige, sur deux orthostiches (figures 35 à 38). L’angle de divergence mesure en moyenne 180°. Cette phyllotaxie, modélisée sur la figure 90, est fréquente chez les Monocotylédones, plus rare chez les Dicotylédones (tilleul, orme, vigne, etc.).
10.1.2c Phyllotaxie alterne tristique
Les feuilles sont réparties sur trois orthostiches disposées en étoile autour de la tige (figure 39). L’angle de divergence mesure en moyenne 120°. Cette phyllotaxie, habituelle chez les Cypéracées, est modélisée sur la figure 91.
10.1.2d Phyllotaxie alterne pentastique
Les feuilles se répartissent sur cinq orthostiches disposées en étoile autour de l’axe de la tige, décalées (de proche en proche) de 72° ; l’angle de divergence mesure en moyenne 144°. Cette très rare phyllotaxie, modélisée sur la figure 92, s’observe sur Aloe juvenna (figure 40). Elle est exceptionnellement observée sur certains spécimens dont la phyllotaxie est habituellement alterne spiralée standard, tel Sonchus asper, non illustré.
10.1.2e Phyllotaxie alterne octostique
Les feuilles se répartissent sur huit orthostiches disposées en étoile autour de l’axe de la tige, opposées deux par deux dans quatre plans faisant entre eux des angles de 45° ; l’angle de divergence mesure en moyenne 135°. Cette phyllotaxie exceptionnelle s’observe sur Euphorbia obesa (figure 41, à gauche), mais aussi sur Astrophytum asterias (non illustré). Bel exemple de convergence évolutive entre une Euphorbiacée sud-africaine et une Cactacée américaine ! Cette phyllotaxie est modélisée sur la figure 94.
10.2. Phyllotaxies opposées : deux feuilles par nœud
Dans chaque paire de feuilles opposées, l’angle de divergence mesure en moyenne 180°. Un entrenœud court alterne avec un entrenœud long.
10.2.1 Phyllotaxie opposée distique
Les paires de feuilles sont toutes dans un même plan passant par l’axe de la tige (figure 42). Cette phyllotaxie est modélisée sur la figure 96.
10.2.2 Phyllotaxie opposée décussée
Chaque paire de feuilles est décalée de 90° par rapport à la paire précédente. Vues dans l’axe de la tige, les feuilles sont disposées sur quatre rangées en croix, opposées deux par deux dans deux plans perpendiculaires (figure 43). Cette phyllotaxie est modélisée sur la figure 97.
Les feuilles de Salix purpurea sont habituellement opposées décussées (figure 45, à droite) mais cette espèce porte souvent des paires de feuilles subopposées (figure 45, à gauche). Dans une même paire de feuilles subopposées, l’entrenœud est court, alors que, dans une même paire de feuilles opposées, l’entrenœud est nul.
La figure 46 illustre la phyllotaxie opposée décussée sur les pièces florales du Coquelicot.
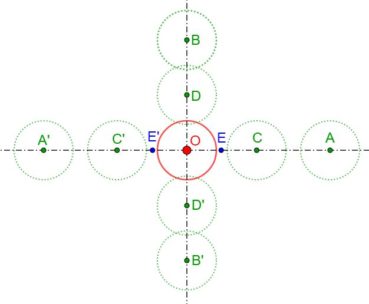
10.2.3 Phyllotaxie opposée multijuguée
Vue dans l’axe de la tige, chaque paire de feuilles est décalée, par rapport à la précédente, d’un angle moyen de 68,75°, moitié de l’angle d’or (figures 47 et 48). Cette phyllotaxie est modélisée sur la figure 98.
10.3. Phyllotaxies verticillées : au moins trois feuilles par nœud
Dans chaque verticille, l’angle de divergence est un diviseur entier de 360°. Au moins deux entrenœuds très courts ou nuls alternent avec un entrenœud long.
Les phyllotaxies verticillées s’observent surtout sur les pièces florales, pour lesquelles les alignements radiaux concernent peu de verticilles. On ne les rencontre jamais sur un capitule, car elles ne permettraient pas aux fleurons d’occuper l’espace disponible de manière optimale.
10.3.1 Verticilles de trois feuilles : phyllotaxie verticillée tristique
Dans chaque verticille, les feuilles sont groupées par trois, avec un angle de divergence moyen de 120° ; deux verticilles consécutifs sont décalés de 60° (figures 49 et 50). Cette phyllotaxie est modélisée sur la figure 99.
Phyllotaxie verticillée tristique des pièces florales des Monocotylédones
Chez les Monocotylédones, les fleurs sont habituellement trimères (figure 51). Chaque fleur présente alors deux verticilles superposés, séparés par un entrenœud très court ou nul : un verticille de trois sépales, un autre de trois pétales (soit au total six tépales lorsque les sépales et les pétales sont fortement semblables), un verticille de trois ou six étamines et un ovaire à trois ou six loges.
Le verticille des pétales et celui des sépales sont très rapprochés, décalés l’un par rapport à l’autre de 60°. Sépales et pétales peuvent être de même taille, mais les sépales sont souvent un peu plus grands que les pétales (figure 51, à droite).
10.3.2 Verticilles de quatre feuilles : phyllotaxie ventriculée, ou verticillée tétrastique
Dans chaque verticille, les feuilles sont groupées par quatre, avec un angle de divergence moyen de 90° ; deux verticilles consécutifs sont décalés, l’un par rapport à l’autre, de 45°. Cette phyllotaxie peu fréquente est modélisée sur la figure 100.
Rare sur les feuilles, la phyllotaxie ventriculée s’observe sur les pièces florales des fleurs tétramères des Brassicacées, de certaines Onagracées, de la Parisette à quatre feuilles.
- Chez les Brassicacées (figure 55), les fleurs portent quatre sépales et quatre pétales en croix, d’où leur ancien nom de Crucifères.
- Chez les Onagracées, par exemple chez Epilobium dodonaei fleischeri (figure 56 à gauche), les fleurs présentent le plus souvent quatre sépales et quatre pétales (décalés de 45° par rapport aux sépales), huit étamines, quatre stigmates en croix, une capsule qui s’ouvre par quatre valves. Mais Circaea lutetiana (figure 56 à droite) a seulement deux sépales, deux pétales (profondément échancrés) et deux étamines. Les Ludwigia (non illustrés) peuvent avoir, selon les espèces, de quatre à six sépales, et de zéro à six pétales.
- Chez Paris quadrifolia (figure 57), toutes les bractées et les pièces florales sont vertes, à l’exception de l’ovaire, qui est noir. Au-dessus des quatre grandes bractées foliacées, la fleur présente quatre sépales lancéolés, quatre pétales filiformes, huit étamines, un ovaire puis une capsule à quatre stigmates et quatre loges. Mais l’auteur a aussi photographié, une seule fois, une parisette « à cinq feuilles » (non représentée).
10.3.3 Verticilles de cinq feuilles : phyllotaxie verticillée pentastique
Dans chaque verticille, les feuilles (ou les pièces florales) sont groupées par cinq, avec un angle de divergence moyen de 72° ; deux verticilles consécutifs sont décalés, l’un par rapport à l’autre, de 36°. Cette phyllotaxie est modélisée sur la figure 101. Elle s’observe chez certains Myriophylles (Myriophyllum verticillatum, M. aquaticum, espèces non représentées), dont les feuilles peuvent aussi, sur une même tige, être verticillées par quatre ou par six. Elle s’observe aussi chez Erica vagans, dont les feuilles peuvent aussi être verticillées par quatre.
La phyllotaxie verticillée pentastique s’observe bien plus fréquemment sur les pièces florales des nombreuses Dicotylédones dont les fleurs sont pentamères. Le plus souvent, ces fleurs ont cinq sépales, cinq pétales, cinq ou dix étamines, avec présence éventuelle de cinq nectaires bien développés (figures 58 et 59).
10.3.4 Verticilles de six feuilles : phyllotaxie verticillée hexastique
Dans chaque verticille, les feuilles sont groupées par six, avec un angle de divergence moyen de 60° ; deux verticilles consécutifs sont habituellement décalés, l’un par rapport à l’autre, de 30° (figure 60). Cette rare phyllotaxie est modélisée sur la figure 102.
11. Variabilité de la phyllotaxie
Les changements de phyllotaxie déjà signalés chez le Laurier-rose (figure 50) et chez l’Orpin pourpier (figures 52 et 53) ne sont pas exceptionnels. La phyllotaxie d’une espèce n’est pas toujours constante, aussi bien sur un même spécimen que sur deux spécimens différents. Elle dépend de la vigueur de la tige (et de ses rameaux) au cours de la croissance.
La figure 61 montre deux rameaux voisins d’un même spécimen d’Olea europaea, dont la phyllotaxie est normalement opposée décussée, mais qui peut très exceptionnellement être verticillée tristique.
La figure 62 montre plusieurs rameaux d’un même spécimen de Punica granatum, dont la phyllotaxie est normalement opposée décussée. Exceptionnellement et sur certains rameaux, elle peut être alterne spiralée ou verticillée tristique.
La figure 63 montre un pied de la méditerranéenne Veronica cymbalaria. La tige porte à sa base une à trois paires de feuilles opposées, à l’aisselle desquelles naissent des rameaux – eux-mêmes ramifiés – qui s’entremêlent, chacun portant habituellement une seule paire de feuilles opposées. Au-dessus de ces feuilles opposées, les prolongements de la tige et des rameaux sont des inflorescences, dont les « feuilles » (en réalité des bractées foliacées en tous points semblables à des feuilles) sont alternes, avec des entrenœuds de longueurs variables, certaines subopposées, sinon alternes. Les fleurs sont solitaires, longuement pédicellées. Les corolles, d’un blanc pur, se détachent facilement et tombent au sol (points blancs sur la photo).
La figure 64 montre les rameaux d’une branche de Diopyros lotus photographiés dans le jardin de l’auteur : d’alterne spiralée à la base, la phyllotaxie devient rapidement alterne distique.
Les figures 65 et 66 montrent la phyllotaxie particulière d’un Eucalyptus, probablement Eucalyptus globulus du fait que l’écorce des rejets plus âgés se détache en bandes longitudinales restant longtemps en partie attachées au tronc (figure 65, à droite). Les jeunes rejets, habituellement dressés, ont une phyllotaxie très majoritairement opposée distique. Cependant, sur le rejet de la figure 65 à gauche, et au milieu de cinq paires de feuilles opposées distiques, on observe une paire de feuilles opposées décussées (flèche blanche). Toutes les feuilles des autres jeunes rejets voisins sont opposées distiques. Les rameaux portés par des branches âgées (figure 66) sont pour la plupart horizontaux ou pendants, et leur phyllotaxie est habituellement alterne distique, avec passage occasionnel à une phyllotaxie alterne monostique.
Chez Diospyros lotus et chez l’Eucalyptus commun, les rameaux portés par de jeunes tiges (ou par des rameaux en début de croissance) sont dressés, alors que les rameaux portés par des branches âgées sont pendants ou le deviennent en cours de croissance. La phyllotaxie de ces rameaux semble liée à leur orientation au cours de leur croissance.
La figure 67 montre deux pieds de Lilium martagon, photographiés dans le même secteur du Parc national de la Vanoise. Sur l’un, les feuilles sont verticillées par cinq à neuf, alors que sur l’autre elles sont alternes spiralées et disposées en hélice irrégulière.
Des variations de phyllotaxie s’observent parfois sur les pièces florales de deux fleurs voisines portées par un même spécimen (figure 68).
Ces exemples n’ont rien d’exceptionnel : parmi les espèces illustrées sur les figures 26 à 68, plus de quarante ont été photographiées dans le jardin de l’auteur ou à moins de vingt kilomètres de son domicile et, parmi celles-ci, au moins une dizaine d’entre elles a présenté des variations de phyllotaxie. D’autres phyllotaxies plus rares peuvent être observées (Bell & Bryan, 1991 ; Rowe-Pirra, 2019), etc.
12. Croissance des végétaux et phyllotaxie
12.1. Le développement des êtres vivants
Une citation extraite du livre Tous entrelacés ! par Éric Bapteste (2018) éclairera ce qui suit : « Ce qui différencie une drosophile d’un renard, un papillon d’un lion, un ver d’une baleine, un singe d’un homme, ce ne sont pas leurs gènes, mais l’ordre, le moment et le tissu dans lequel ces gènes sont déployés, sous l’influence des molécules régulatrices ».
Les gènes d’un être vivant contiennent le plan général de son développement, qui détermine, dans un processus auto-organisé, l’ordre et le mode de formation et de développement des différents organes, et dans chaque organe la différenciation et la répartition spatiale de ses cellules spécialisées. Cependant, il n’en fixe les ultimes détails que statistiquement et de manière partiellement aléatoire : pour chaque individu, le devenir de chaque cellule est simultanément contrôlé par son programme génétique, par les interactions avec les cellules voisines, par l’environnement dans lequel elle se développe (figure 69).
Le fait que nous ayons des empreintes digitales est héréditaire, mais pas les détails de leurs circonvolutions. Les vrais jumeaux ont des empreintes digitales différentes et, pour chacun de nous, les empreintes de chaque doigt sont différentes. C’est pour cela qu’elles permettent de nous identifier, tout comme les proportions de notre visage, notre réseau sanguin ou l’iris de nos yeux. Même chose pour les taches des léopards et des girafes, pour les rayures des zèbres et des tigres, dont la formation peut être simulée sur ordinateur.
Ce plan général pourrait être comparé aux règles qui définissent un automate cellulaire mais il en diffère. Un automate cellulaire est entièrement déterministe : de mêmes conditions initiales conduisent toujours au même résultat, ce qui ne laisse aucune place au hasard.
Les automates cellulaires ont fait leur apparition dès le début de l’informatique. Le plus connu est le « jeu de la vie », imaginé par John Conway en 1970. Dans le « jeu de la vie », un petit nombre de règles simples détermine le comportement de chaque « cellule » d’un quadrillage du plan. Le jeu se déroule par étapes successives : une « cellule » évolue en fonction de son état antérieur et de l’état des cellules voisines (voir règles et animations sur Internet).
Gaston Bonnier (1853-1922), éminent botaniste, est l’auteur de plusieurs flores réputées, dont la Flore complète illustrée de France, Suisse et Belgique et la Flore complète portative de la France, de la Suisse et de la Belgique. Il y a plus d’un siècle, il a mis en évidence que des plantes alpines ont un aspect parfois très différent selon qu’elles sont observées dans les conditions naturelles de la haute montagne ou cultivées dans le Jardin des plantes de Paris. Leurs caractères floraux (héréditaires) ne sont globalement pas changés, mais leur taille, le développement de leur tige et de leurs feuilles, leur période de floraison sont tellement différents que l’on pourrait croire que ce sont des espèces différentes : cultivé en plaine, l’Edelweiss (figure 119) n’a pas l’épaisse pilosité blanche et cotonneuse qu’il porte en haute montagne et qui le protège à la fois de l’intensité du rayonnement solaire et des fortes différences de température entre le jour et la nuit.
12.2 Le développement des végétaux
Une jeune tige porte à son sommet un méristème, plus petit qu’une pointe d’épingle, comprenant au plus quelques dizaines de cellules et qui assure sa croissance (de même pour une jeune racine, mais ce n’est pas notre sujet). Le méristème est habituellement en forme de dôme ou d’ogive (figures 72 et 73), dont le sommet est l’apex.
Aucune feuille ne peut se former à l’apex d’un méristème, qui dans un premier temps assure prioritairement le développement de la tige, ensuite qui se termine le plus souvent par une fleur ou par une inflorescence. Les cellules du méristème se multiplient, puis se différencient lorsqu’elles s’éloignent de l’apex, par un mécanisme qui permet simultanément la croissance de la tige et des organes qu’elle porte. Chacun de ces organes est issu d’un minuscule renflement de cellules en division, appelé primordium (au pluriel primordia), qui se forme en bordure du méristème.
Le processus se reproduit de manière récursive sur les éventuelles ramifications de la tige (ou de la racine, dont le développement suit un processus comparable), qui développent leurs propres méristèmes. Il s’arrêtera de manière génétiquement programmée et en fonction des contraintes du milieu de vie.
Les cellules du méristème se divisent et se différencient – de manière auto-organisée – en présence d’activateurs et d’inhibiteurs de croissance. Nous le verrons par la suite, le principal de ces activateurs est l’auxine, qui induit la croissance en un point où elle est concentrée, mais d’autres activateurs et divers inhibiteurs, aussi bien chimiques que physiques, ont été mis en évidence (voir page 44).
En plus de leur sensibilité à différentes phytohormones, les cellules des plantes sont sensibles à la pression exercée par les cellules voisines et aux signaux chimiques qu’elles émettent (par simple contact ou proximité), à la gravitation terrestre, à la direction moyenne aussi bien qu’à l’intensité, la périodicité et la composition spectrale de la lumière qu’elles reçoivent, aux variations saisonnières ou journalières de température et d’humidité, à l’altitude, aux contraintes imposées par les vents, au type de sol et à la biodiversité qu’il abrite, à la composition de leur microbiote aérien ou racinaire, aux interactions avec des bactéries, des virus, des champignons, d’autres plantes voisines, des animaux… Tous ces facteurs entrent en jeu dans les associations phytosociologique dans lesquelles peuvent être regroupées les espèces de mêmes affinités, que l’on rencontre souvent ensemble.
La figure 162 illustre le comportement des jeunes vrilles de Bryone. Si l’une d’elles s’approche d’un support auquel elle est susceptible de s’enrouler, les cellules au contact de l’obstacle ralentissent leur développement, alors que celles du côté opposé conservent un développement normal. Le signal se propage unilatéralement vers l’extrémité de la vrille, qui s’enroule autour de l’obstacle.
À moins que sa croissance soit indéfinie, la tige sera habituellement terminée par une fleur unique (tulipe ; figure 51) ou par une inflorescence (figure 30), et il en est de même pour ses éventuelles ramifications. Sinon, la tige principale continue sa croissance et son développement l’emporte toujours, au moins en début, sur la croissance des organes latéraux.
Chez les espèces herbacées volubiles, vivaces mais à tiges annuelles, comme Dioscorea communis ou Bryonia dioica, les inflorescences sont axillaires et naissent d’un bourgeon à l’aisselle des feuilles. La croissance de la tige est continue et ne s’arrête d’elle-même qu’après la période de floraison.
Chez les plantes herbacées, aucune feuille ne se forme entre deux feuilles précédemment formées ni sur une autre feuille et, si des rameaux se développent par la suite, ils seront issus de bourgeons en dormance à l’aisselle des pétioles des feuilles.
Cependant, chez certaines espèces de Kalanchoe ou de Bryophyllum malgaches, à feuilles charnues, des propagules se développent sur la marge du limbe et assurent une reproduction végétative.
Chez de nombreuses espèces d’arbres à feuilles caduques (saules, peupliers, tilleuls, etc.) mais habituellement pas chez les conifères, il est fréquent que des bourgeons évoluant en rameaux se développent directement à partir de bourgeons dormants sous l’écorce des troncs et des branches, surtout lorsque ces arbres ont été taillés. Ces bourgeons sont générés par un méristème secondaire, qui permet la croissance en diamètre du tronc de l’arbre. C’est ce phénomène qui permet aux « trognes » de régénérer leurs branches après une taille sévère.
Chez le cacaoyer et l’arbre de Judée, les inflorescences elles-mêmes se développent directement sur des renflements de l’écorce du tronc ou des branches.
Chez certains arbres, et au-delà d’un certain développement, les branches prennent le relais de la tige principale, qui n’est plus nettement distincte de ses branches. C’est le cas chez le Cèdre du Liban, lorsqu’il atteint un âge suffisant. La structure générale de l’arbre peut devenir fractale, c’est-à-dire invariante par changement d’échelle (figure 70).
12.3. Évolution des connaissances sur la phyllotaxie
Des observations de W. Hofmeister à la théorie du plus grand espace disponible de M. et R. Snow
En 1868, en se fondant sur ses observations microscopiques, W. Hofmeister a prouvé que chaque primordium se forme dans une toute petite zone, en bordure du sommet de l’apex du méristème, entre celui-ci et les primordia déjà formés.
Au milieu du xxe siècle, M. et R. Snow ont développé une théorie mécanique dynamique de la formation des primordia, appelée théorie du plus grand espace disponible : « une feuille naît dans le territoire de l’apex qui atteint le premier une largeur minimale et un certain éloignement de l’extrémité apicale ». Cette théorie purement mécaniste a été complétée par les interprétations physiologiques de différents auteurs (Schoute, Richards, Wardlaw) qui, suite aux travaux d’Alan Turing, font intervenir des gradients dans la concentration de différentes hormones, au voisinage de l’apex et des primordia déjà formés (figures 71, 72 et 73).
Alan Turing, génial mathématicien anglais, a développé en 1952 un modèle mathématique de réaction-diffusion permettant d’expliquer la formation auto-organisée de structures périodiques dans de nombreux systèmes biologiques. Célèbre pour être le fondateur de l’informatique moderne, il est moins connu du public pour avoir construit, avec deux de ses collègues de Cambridge, l’un des premiers ordinateurs, la « Bombe », qui lui a permis de casser le code réputé inviolable utilisé par l’armée nazie, encodé avec la machine Enigma. Grâce à cet exploit, qui n’a été révélé que 25 ans plus tard, le débarquement a pu avoir lieu le 6 juin 1944, avant que les nazis n’aient eu le temps de finir la mise au point de leur bombe atomique, qui aurait été portée par les fusées V2. L’un des principaux acteurs de la victoire de 1944 était donc un mathématicien. Décédé en 1954 dans des circonstances qui auraient pu et dû être évitées, Alan Turing n’a pas eu de son vivant la reconnaissance qu’il méritait : il n’a été réhabilité et reconnu comme héros de guerre qu’en 2013, presque 70 ans après la capitulation du 8 mai 1945 qui a marqué la fin de la guerre.
Ces travaux ont été progressivement complétés par ceux de différents universitaires. Pour ne citer qu’eux : Lucien Plantefol et Jean-Edme Loiseau en France, Roger V. Jean au Canada, plus récemment l’Anglais Adrian D. Bell. Ces différents auteurs ont établi que l’apex du méristème et les primordia déjà formés ont une action inhibitrice : comme nous l’avons dit ci-dessus, aucun primordium ne peut se former à l’apex lui-même ni à proximité immédiate d’un autre primordium déjà formé. Cette action inhibitrice décroît avec la distance, ce qui suggère un phénomène de diffusion. Les primordia déjà formés s’éloignent radialement de l’apex et les uns des autres, et un nouvel espace de moindre inhibition apparaît régulièrement à proximité de l’apex.
L’expérience de Yves Couder et Stéphane Douady (1993-1996)
Au laboratoire de Physique statistique de l’École normale supérieure, Yves Couder et Stéphane Douady ont imaginé le dispositif suivant :
- un plateau circulaire, muni en son centre d’une petite protubérance et baignant dans l’huile, est placé dans un champ magnétique radial, d’intensité modulable, maximale à la périphérie du disque ;
- des gouttes de ferro fluide (poudre fine d’oxyde de fer en suspension) sont déposées au centre du plateau, à une fréquence modulable.
Lorsqu’une goutte tombe, elle ne peut pas rester au centre du plateau, dont elle s’éloigne radialement sous l’effet du champ magnétique. Simultanément sous l’effet de ce dernier, les gouttes sont polarisées et se repoussent entre elles : une nouvelle goutte se place spontanément dans le plus grand espace disponible. Et là, surprise ! Lorsque certaines conditions sont réunies, chaque goutte s’insère dans un motif régulier, dans lequel (comme sur les capitules des Asteracées) interviennent l’angle d’or et les suites de Fibonacci. Ce motif dépend de plusieurs paramètres, entre autres :
- la forme de la protubérance, au centre du plateau,
- la fréquence avec laquelle on fait tomber les gouttes,
- la vitesse avec laquelle les gouttes s’éloignent du centre.
12.4. L’interprétation actuelle
Toutes ces avancées, en particulier l’expérience de Yves Couder et Stéphane Douady, ont permis de modéliser la formation et la croissance des primordia, futures feuilles ou pièces florales, par un processus unique, dynamique et auto-organisé. Ce processus est génétiquement programmé pour chaque espèce (ou groupe d’espèces) végétale. Il est régulé par un jeu complexe d’activateurs et d’inhibiteurs, susceptible d’être modulé par les conditions de croissance. Bien qu’il reste encore de nombreux points à préciser, il permet de modéliser les phyllotaxies habituellement observées.
Voici, en résumé, les règles simplifiées qui, pour l’instant, définissent cette interprétation.
Aucun primordium ne se forme à l’apex du méristème de la tige en croissance (sauf éventuellement celui d’un bourgeon floral qui terminera la tige) ni à l’emplacement d’un autre primordium déjà formé.
Une explication probable est que, par un phénomène de diffusion, l’apex et les primordia privent d’auxine les cellules proches, ce qui définit à leur voisinage immédiat une zone d’inhibition empêchant toute formation d’un nouvel organe.
Chaque primordium se forme en bordure du méristème, puis s’en éloigne radialement au cours de sa croissance, sans changer sa direction initiale. Une fois le processus engagé, les primordia déjà formés s’éloignent simultanément du méristème et les uns des autres, libérant périodiquement un nouvel espace de moindre inhibition, ou « plus grand espace disponible », dans lequel un nouveau primordium peut se former.
La formation et la croissance des primordia dépendent des concentrations locales en auxine (la principale phytohormone, qui active la division des cellules végétales) et en d’autres phytohormones comme les cytokinines (qui stimulent la division cellulaire et induisent le développement des bourgeons qui se formeront à l’aisselle des futures feuilles) et les gibbérellines (qui agissent sur l’élongation des entrenœuds), et probablement de la pression localement exercée par les cellules voisines lors de leur croissance.
Les concentrations locales en ces diverses phytohormones sont liées à la fréquence d’apparition des primordia, à la taille des zones d’inhibition qu’ils engendrent, à leur vitesse de croissance, à la vitesse à laquelle ils s’éloignent du méristème et les uns des autres, mais aussi à la fréquence et à la répartition des entrenœuds, modulées par une protéine nommée AHP6, dont une forte concentration inhibe les cytokinines (Besnard, 2011).
Dans les phyllotaxies alternes, les entrenœuds sont régulièrement espacés. Dans les phyllotaxies opposées, un entrenœud très court ou nul alterne avec un entrenœud long. Dans les phyllotaxies verticillées, au moins deux entrenœuds très courts ou nuls alternent avec un entrenœud long. La phyllotaxie peut dépendre du stade, de la vitesse et de la vigueur de croissance de la tige principale et de ses éventuels rameaux, mais peut-être aussi de leur orientation par rapport à la gravité terrestre ou à la source de lumière (figures 61 à 68).
Ce processus se prête à des simulations informatiques. Celles qui sont proposées par Boissière (2000) et par Rousseau & Zazoun (2008) rendent bien compte des observations, mais elles utilisent des notions mathématiques dépassant largement les connaissances des lycéens, ainsi que des logiciels spécialisés, comme Maple. C’est pourquoi des simulations simplifiées sont proposées dans ce qui suit : elles n’utilisent que le logiciel libre Geogebra, bien connu des lycéens, tout en rendant assez bien compte des caractéristiques des différentes phyllotaxies, du moins tant que la croissance de la plante reste régulière et continue.
13. Croissance des végétaux et phyllotaxie
13.1. Phyllotaxies alternes : une seule feuille par nœud
13.1.1 Phyllotaxie alterne spiralée standard
Pour construire les figures 75_1 à 75_13 et les figures 89 à 102 à l’aide de Geogebra :
- placer un point au centre du repère et le renommer O ; tracer le cercle (C) de centre O et de rayon donné, de longueur 1 sur la figure 75, mais ce choix est arbitraire ;
- placer un point A sur l’axe des abscisses, juste à l’extérieur de (C), puis un cercle de centre A et de même rayon que le précédent ; un rayon différent modifie la vitesse d’éloignement des primordia ;
- partant de A et de O, construire un « angle de mesure donnée ». Pour la phyllotaxie alterne-spiralée standard, cette mesure sera de 137,5°. Le point obtenu, automatiquement appelé A1 par Geogebra, définit l’angle (
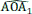 ) dont la mesure s’affiche sur la figure ;
) dont la mesure s’affiche sur la figure ; - éloigner le point A du point O : le point A1 s’éloigne à la même distance du point O ;
- tracer la demi-droite [OA1] et placer sur cette demi-droite, juste à l’extérieur du cercle (C), un point B. Ensuite, pour alléger la figure, sélectionner le point A1 puis décocher la case « afficher l’objet ». Idem pour l’angle
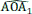 . Attention de ne pas supprimer ces deux éléments, le lien entre le point A et les suivants serait perdu… ;
. Attention de ne pas supprimer ces deux éléments, le lien entre le point A et les suivants serait perdu… ; - recommencer selon le même processus. Tous les points suivants seront alors liés au point A et, lorsqu’on éloigne le point A du point O, tous les points créés s’éloignent de O de manière proportionnelle, en se répartissant automatiquement sur une spirale exponentielle.
13.1.1a Formation des organes
- Après formation d’un premier primordium, un deuxième primordium se développe habituellement à l’opposé du premier par rapport à l’apex, donc avec un angle de divergence proche de 180°.
- Un troisième primordium se formera avec un angle de divergence inférieur à 180° : il n’est habituellement pas exactement à l’opposé du deuxième car il serait trop proche du premier, celui-ci n’étant pas encore assez éloigné de l’apex.
- Pour les primordia suivants, un angle de divergence statistiquement constant apparaît. Le processus conduit le plus souvent à un angle moyen de divergence égal à l’angle d’or, de mesure approchée 137,5° (d’autres valeurs sont possibles), et les primordia suivants se répartissent spontanément le long d’une spirale générative dont les caractéristiques générales dépendent de différents facteurs (forme de l’apex, vitesse de formation et de croissance des primordia, vitesse et condition de croissance de la tige, etc.).
- Cette spirale générative est initialement et a priori une spirale exponentielle (figure 75_13), la seule qui permette aux organes de se former et de grandir sans changer de forme.
Cependant, lorsque les organes issus des primordia (feuilles sur une tige ou fleurons sur un capitule) s’éloignent du méristème, leur vitesse de croissance varie et les caractéristiques de la spirale se modifient. Une spirale exponentielle ne peut modéliser la phyllotaxie que pendant les phases de formation et de croissance régulière des organes.
- Sur une tige qui s’allonge en cylindre, la spirale exponentielle initiale se transforme rapidement en hélice, de « pas » plus ou moins régulier, qui entoure la tige (figures 27 et 28). Le pas d’une hélice est la distance entre deux spires, mesurée parallèlement à l’axe.
- Sur un capitule presque plan, comme chez le tournesol, la spirale générative se rapproche progressivement d’une spirale d’Archimède lorsque les fruits périphériques (issues des premiers fleurons formés) approchent puis atteignent leur taille maximale (figure 109).
- Lorsque les organes (feuilles sur une tige, fleurs sur une inflorescence en grappe ou fleurons sur un capitule) sont nombreux et serrés, on voit apparaître des parastiches, spirales secondaires qui s’entrecroisent, et dont le nombre dépend des conditions précédentes.
Certaines parastiches s’enroulent dans le sens anti-horaire, que nous noterons (a-h), d’autres dans le sens horaire, que nous noterons (h). Les nombres de parastiches sont a priori des termes de la suite de Fibonacci, étroitement liée à l’angle d’or. Dans les rares exceptions (illustrées figures 127 et 128), ce sont les termes de suites définies par l’algorithme de Fibonacci, qui ne diffèrent de la suite de Fibonacci que par la valeur de leurs deux premiers termes.
Le nombre de parastiches semble lié au rythme d’apparition et à la vitesse de croissance des primordia, ainsi qu’au diamètre de la zone d’inhibition autour de chaque nouveau primordium, et ces paramètres peuvent varier dans le temps (Boissière, 2000). Sur les capitules des Asteracées (figures 103 à 117), ce rythme est initialement faible, puis il s’accélère : les parastiches sont plus nombreuses, plus visibles et plus régulières à la périphérie du capitule, où se regroupent les premiers fleurons formés. Vers le centre du capitule, elles sont progressivement moins nombreuses puis moins régulières (figures 109 à 113). Tout au centre, elles disparaissent : les fleurons sont en partie avortés, probablement par manque de place pour se développer. Dans les modélisations proposées page 48 et suivantes, les spirales 1 et 2, associées à une croissance rapide, ont des spires espacées et elles présentent moins de parastiches que les spirales 4 et 5, associées à une croissance lente, aux spires plus serrées. Les figures 104 à 117 en donnent des exemples.
13.1.1b Comment expliquer que, dans la phyllotaxie alterne-spiralée, l’angle de divergence soit le plus souvent égal à l’angle d’or et que, dans les autres phyllotaxies, cet angle reste lié à l’angle d’or ?
Nous savons que la valeur prise par l’angle de divergence s’explique par le processus auto-organisé de formation des primordia. Une disposition trop symétrique ne permet pas à ceux-ci d’occuper le voisinage de l’apex de manière optimale lorsque les organes qui en sont issus sont nombreux et restent groupés au cours de leur croissance. Il peut s’agir des feuilles d’une rosette basale qui, tout en restant serrées, devront toutes avoir accès à la lumière. Il peut s’agir des fleurs nombreuses portées par une inflorescence en grappe dense ou en capitule qui, tout en restant serrées, devront remplir au mieux l’espace disponible, sans laisser de vides.
- Lorsque l’angle de divergence est un diviseur entier de 360° (pages 55 à 61), les primordia se répartissent naturellement sur des orthostiches, alignements radiaux qui laissent entre eux, lorsqu’ils s’éloignent du méristème, des espaces libres de plus en plus grands.
- Au contraire, lorsque l’angle de divergence est irrationnel, les primordia, et ensuite les organes qu’ils initient, peuvent se développer en occupant l’espace disponible sans laisser de vides. Ceci concerne aussi bien les feuilles nombreuses et serrées portées par une rosette (figure 74) ou par une tige courte (figure 126), qui peuvent ainsi toutes accéder équitablement à la lumière, que les fleurs d’une inflorescence en grappe (figure 30) ou en capitule (figures 103 à 119), qui peuvent se développer librement tout en conservant une densité maximale sur une surface minimale. Ces conditions sont réalisées de manière optimale lorsque l’angle de divergence est l’angle d’or, dont la mesure est la plus irrationnelle des mesures d’angles, de même que est le nombre le plus irrationnel de tous les nombres irrationnels.
L’évolution est économe. La phyllotaxie alterne spiralée est un bon exemple d’utilisation naturelle et spontanée, tout au long de l’évolution, du « principe de parcimonie » : entre plusieurs possibilités et dans un contexte donné, l’évolution a retenu le mécanisme qui est théoriquement le plus cohérent, le plus simple, le plus efficace, le plus économe.
13.1.1c Image par image, formation des douze premiers organes dans la phyllotaxie alterne spiralée standard
Les figures suivantes ont été réalisées à l’aide du logiciel Geogebra selon le processus décrit page 44 :
- chaque point est au centre d’un disque qui matérialise une zone d’inhibition ;
- le point rouge O représente l’apex du méristème ;
- chaque point vert représente un nouveau primordium, ensuite l’organe qui en est issu ;
- à chaque étape, le point bleu se trouve dans le plus grand espace disponible et indique le lieu de formation du prochain primordium.
L’éloignement radial de A par rapport à O induit automatiquement l’éloignement radial, proportionnel, de chacun des points suivants par rapport à O.
13.1.1d Cas particulier des capitules des Asteracées
Pour modéliser de manière simplifiée la phyllotaxie alterne spiralée associée à l’angle d’or, telle qu’observée sur les capitules des Asteracées, deux hypothèses simples suffisent :
- vus du dessus et dans l’axe de la tige, les fleurons se forment l’un après l’autre sur une spirale générative de centre O ; au voisinage de l’apex du méristème, celle-ci est une spirale exponentielle ;
- l’angle de divergence entre deux fleurons successivement formés est l’angle d’or, de mesure approchée 137,5°.
Ces deux hypothèses sont à la fois compatibles entre elles et compatibles avec une formation et une croissance auto-organisées et autosimilaires des fleurons, qui peuvent se former et grandir de manière continue, sans changer de forme tant qu’ils sont en croissance, et en conservant une densité maximale (page 61). Cette modélisation est valable tant que la vitesse d’éloignement des fleurons peut être considérée comme constante. Pour une modélisation tenant compte des variations dans la vitesse de formation et de croissance des fleurons, et leur vitesse d’éloignement du centre, voir Boissière (2000) et Rousseau & Zazoun (2008).
Sur les figures 76 à 88, les spirales génératives ont été tracées avant de placer les points représentant les primordia et les fleurons qui en sont issus. Ces spirales ont pour centre l’apex O du méristème et elles sont privées de leur zone centrale, qui peut être assimilée à la zone d’inhibition de ce dernier. Les points qu’elles portent représentent des primordia, les derniers formés étant les plus proches du centre.
La mesure de l’angle d’or étant irrationnelle, ce modèle ne donnera jamais deux fleurons exactement alignés sur une même demi-droite passant par le centre du méristème. Toutefois, en acceptant des imprécisions compatibles avec les mesures des angles et les variations aléatoires de la position des fleurons, nous retrouverons les observations classiques sur les indices de phyllotaxie.
Dans cette modélisation, les spirales sont d’autant plus serrées que le rythme d’apparition et la vitesse de développement des primordia sont lents et que la zone d’inhibition de ces derniers est réduite. Nous construirons les cinq spirales d’équations polaires respectives :
r = et/20, r = et/40, r = et/80, r=et/120, r = et/240
De par leurs équations, ces spirales s’enroulent toutes dans le sens anti-horaire (sens trigonométrique positif). La spirale d’équation r = – et/20 , isométrique à la première dans une symétrie de centre O, s’enroulerait dans le sens horaire.
À chaque spirale, nous associerons au moins un indice de phyllotaxie, qui dépendra de la précision avec laquelle les fleurons peuvent être considérés comme approximativement alignés sur une demi-droite passant par le centre O de cette spirale (et du méristème qu’il représente).
Spirale 1
Sur la figure 76, les points A et B (respectivement C et D puis E et F) sont presque alignés sur la demi-droite d1 (respectivement sur les demi-droites d2 et d3). À chaque fois, pour aller d’un point rouge à l’autre, il faut parcourir huit spires et vingt et un entrenœuds. Avec ce choix, l’indice de phyllotaxie est égal à 8/21.
Si on se contentait d’un alignement plus approximatif, en considérant la demi-droite d (en tirets bleus), on passerait d’un point bleu à l’autre en parcourant cinq spires et treize intervalles entre points, ce qui donnerait un indice de phyllotaxie égal à 5/13. La valeur de l’indice de phyllotaxie dépend donc du choix du « bon alignement » choisi, ce qui sera confirmé sur les spirales suivantes.
Une observation attentive de la figure 76 permet de distinguer des parastiches, spirales secondaires qui s’entrecroisent, sur lesquelles s’alignent tous les points de la spirale générative. Ces parastiches ont été matérialisées sur la figure 77 :
- cinq d’entre elles (courbes rouges) s’enroulent dans le sens horaire (h) : un point toutes les deux spires ;
- huit autres (courbes vertes) s’enroulent dans le sens anti-horaire (a-h) : un point toutes les trois spires.
Spirale 2
Sur la figure 78, on observe des points presque alignés sur les demi-droites d1 et d2 (en vert). Pour aller de A à B, ou de C à D, il faut parcourir treize spires et trente-quatre entrenœuds. Avec ce choix, l’indice de phyllotaxie est égal à 13/34.
Une observation attentive de la figure 78 permet de distinguer deux familles de parastiches, matérialisées sur la figure 79 :
- cinq parastiches (h), s’enroulant dans le sens horaire (courbes rouges) : un point toutes les deux spires.
- huit parastiches (a-h), s’enroulant dans le sens anti-horaire (courbes vertes) : un point toutes les trois spires.
Spirale 3
Sur la figure 80, les points I et J sont presque alignés sur la demi-droite d (en vert). Pour aller de I à J, il faut parcourir treize spires et trente-quatre entrenœuds. Avec ce choix, l’indice de phyllotaxie est égal à 13/34.
On pourrait aussi considérer :
- l’alignement approximatif (qui paraît meilleur que le précédent) des points C et D, ou des points E et F, ou encore des points G et H sur les demi-droites respectives d1, d2 et d3 (en rouge). Pour aller d’un point rouge à un autre, il faut parcourir quatorze spires et trente-sept entrenœuds. Avec ce choix, l’indice de phyllotaxie serait égal à 14/37 ;
- l’alignement approximatif des points K et L sur la demi-droite d4 (en violet). Pour aller de K à L, il faut parcourir neuf spires et vingt-trois entrenœuds. Avec ce choix, l’indice de phyllotaxie serait égal à 9/23.
Dans ces deux derniers cas, on rencontre l’une des exceptions à l’universalité apparente de la suite de Fibonacci, signalées par J.-E. Loiseau. Ces exceptions sont décrites par des suites définies par la même relation récurrente que la suite de Fibonacci, un+2 = un+1 + un , mais avec des premiers termes différents : ici 1, 4, 5, 9, 14, 23, 37, etc.
On voit bien que l’on peut se ramener à la suite de Fibonacci en choisissant les points verts sur les demi-droites d. Sinon, nous avons vu (tableau 2) que, pour toute suite définie par l’algorithme de Fibonacci, donc par la relation récurrente un+2 = un+1 + un , la limite du quotient un+1/un est égale à φ. Les phyllotaxies exceptionnelles ci-dessus sont également liées à l’angle d’or.
Une observation attentive de la figure 80 permet de distinguer plusieurs familles de parastiches :
- sur la figure 81, deux familles de parastiches (h), s’enroulant dans le sens horaire : la première formée par les cinq courbes vertes (un point toutes les deux spires) et la seconde formée par les treize courbes rouges (un point toutes les cinq spires) ;
- sur la figure 82, une famille de parastiches (a-h), s’enroulant dans le sens anti-horaire, formée par les huit courbes rouges (un point toutes les trois spires). Pour ne pas alourdir la figure, une autre famille de trois parastiches (a-h) n’a pas été tracée (un point toutes les spires). Voyez-vous ces trois parastiches ?
Spirale 4
Sur la figure 83, les points rouges sur chacune des demi-droites d1, d2, d3 et d4 sont presque alignés. Pour aller d’un point au suivant, il faut parcourir vingt et une spires et cinquante-cinq entrenœuds. Avec ce choix, l’indice de phyllotaxie est égal à 21/55.
Si on se contentait d’un alignement plus approximatif, par exemple les points I et J sur d5, on passerait d’un point vert à l’autre en parcourant treize spires et trente-quatre entrenœuds, ce qui donnerait un indice de phyllotaxie égal à 13/34.
Dans une observation attentive de la figure 83, on distingue plusieurs familles de parastiches,
- sur la figure 84 : deux familles de parastiches (h), la première formée de cinq courbes vertes (un point toutes les deux spires), la seconde formée de treize courbes rouges (un point toutes les cinq spires) ;
- sur la figure 85 : deux familles de parastiches (a-h), la première formée de huit courbes rouges (un point toutes les trois spires) et la seconde formée de vingt et une courbes vertes (un point toutes les huit spires).
Spirale 5
Sur la figure 87, les points O, A et B sont exactement alignés sur la demi-droite d1, alors qu’ils ne devraient pas l’être… et il en est de même pour les points O, C et D sur d2, et des points O, E et H sur d3. En effet : 55 x 360° = 19800°, et 144 x 137,5° = 19800°. L’alignement est dû au fait que 137,5° est une valeur approchée rationnelle de l’angle d’or et non sa valeur exacte, que nous savons être irrationnelle. Sur cette spirale et pour ces deux alignements, l’indice de phyllotaxie est égal à 55/144.
On pourrait se contenter d’alignements plus approximatifs : pour aller de E à F (ou de G à H), on parcourt vingt et une spires pour cinquante-cinq entrenœuds : avec ce choix, l’indice de phyllotaxie serait égal à 21/55. Pour aller de E à G, on parcourt trente-quatre spires pour quatre-vingt-neuf entrenœuds : pour ce choix, l’indice de phyllotaxie serait égal à 34/89. Les alignements sont d’autant meilleurs que les points choisis sont espacés : la détermination de l’indice de phyllotaxie dépend bien du nombre d’organes qui peuvent être pris en compte. Ces valeurs montrent, s’il en était encore besoin, que l’on peut définir plusieurs indices de phyllotaxie pour un même capitule aux fleurons nombreux et serrés, selon le choix et la précision des alignements considérés. On comprend que les différentes phyllotaxies soient actuellement caractérisées par le nombre de feuilles par nœud et l’angle moyen de divergence entre deux organes, plutôt que par le classique indice de phyllotaxie.
Nous avons vu (page 19, tableau 3) que les quotients 8/21, 13/34, 21/55, 34/89 et 55/144 sont des approximations de plus en plus précises de la limite de un/un+2 , quotient de termes d’indices n et n+2 de la suite de Fibonacci. Tous ces différents indices ne sont que des expressions différentes d’une même réalité : nous sommes en présence d’une phyllotaxie liée à l’angle d’or.
Dans une observation attentive de la figure 86, on distingue plusieurs familles de parastiches,
- sur la figure 87 : deux familles de parastiches (h), la première formée treize courbes vertes (un point toutes les cinq spires), la seconde formée de trente-quatre courbes rouges (un point toutes les treize spires) ;
- sur la figure 88 : deux familles de parastiches (a-h), la première formée de huit courbes vertes (un point toutes les trois spires) et la seconde formée de vingt et une courbes rouges (un point toutes les huit spires).
On notera que, sur chacune des figures 87 et 88, les familles de parastiches rouges et vertes déterminent des domaines en forme de losanges curvilignes, dont la forme peut être comparée à celle des semences de tournesol vues de dessus (figure 109).
13.1.1e Précisions sur les relations entre l’angle d’or, la suite de Fibonacci et les indices de phyllotaxie.
Pour chacune des cinq spirales étudiées, récapitulons les nombres de parastiches de même sens et le nombre de spires séparant deux points d’une même parastiche :
- spirale 1 : cinq parastiches (h), points séparés par deux spires, huit parastiches (a-h), points séparés par trois spires ;
- spirale 2 : cinq parastiches (h), points séparés par deux spires, huit parastiches (a-h), points séparés par trois spires ;
- spirale 3 : cinq parastiches (h), points séparés par deux spires, treize parastiches (h), points séparés par cinq spires, huit parastiches (a-h), points séparés par trois spires ;
- spirale 4 : cinq parastiches (h), points séparés par deux spires, treize parastiches (h), points séparés par cinq spires, huit parastiches (a-h), points séparés par trois spires, vingt-et-une parastiches (a-h), points séparés par huit spires ;
- spirale 5 : treize parastiches (h), points séparés par cinq spires, trente-quatre parastiches (h), points séparés par treize spires, huit parastiches (a-h), points séparés par trois spires, vingt-et-une parastiches (a-h), points séparés par huit spires.
Tous ces nombres sont des termes de la suite de Fibonacci. Avec des spirales génératives qui s’enroulent toutes dans le sens anti-horaire, on notera la régularité des valeurs obtenues :
- les nombres de parastiches (h) sont toujours égaux à cinq, treize ou trente-quatre, avec respectivement deux, cinq et treize spires séparant deux points consécutifs d’une même parastiche ;
- les nombres de parastiches (a-h) sont toujours égaux à huit ou vingt-et-un, avec respectivement trois et huit spires séparant deux points consécutifs d’une même parastiche.
Les nombres de parastiches de même sens, ainsi que le nombre de spires séparant deux points d’une même parastiche, sont des termes un et un+2 de la suite de Fibonacci. Y a-t-il un lien avec l’indice de phyllotaxie, exprimé par un quotient de la forme un/un+2 ?
Nous savons (page 6) que l’angle d’or a pour mesure exacte ![]() , où φ est le nombre d’or. Si l’angle de divergence est l’angle d’or α, alors le nombre d’organes par spire est égal à 360/α, quotient de valeur exacte φ², égale à 1+ φ de valeur approchée 2,618. Nous savions déjà que le nombre d’or est étroitement lié à l’angle d’or et à la suite de Fibonacci… Le tableau 4 met en évidence que, si le nombre de spires entre deux organes de même position sur une tige (ou sur un capitule) est égal à un, alors le nombre d’intervalles entre les organes considérés est obligatoirement (et en arrondissant à l’entier le plus proche) égal à un+2.
, où φ est le nombre d’or. Si l’angle de divergence est l’angle d’or α, alors le nombre d’organes par spire est égal à 360/α, quotient de valeur exacte φ², égale à 1+ φ de valeur approchée 2,618. Nous savions déjà que le nombre d’or est étroitement lié à l’angle d’or et à la suite de Fibonacci… Le tableau 4 met en évidence que, si le nombre de spires entre deux organes de même position sur une tige (ou sur un capitule) est égal à un, alors le nombre d’intervalles entre les organes considérés est obligatoirement (et en arrondissant à l’entier le plus proche) égal à un+2.
Dans ce cas, pourquoi l’indice de phyllotaxie n’a-t-il pas été défini comme le seul nombre de spires séparant deux organes de même position sur la tige ? Tout simplement pour éviter des erreurs qui pourraient être dues aux irrégularités entre les mesures des angles individuels de divergence et qui peuvent conduire à des alignements non conformes : sachant que les indices de phyllotaxie sont a priori donnés par la suite de Fibonacci (ou par l’algorithme de Fibonacci), le nombre de spires et le nombre d’organes se contrôlent mutuellement…
13.1.1f Remarques
- Sur les figures 76 à 88, la spirale générative ne serait pas visible si elle n’était pas matérialisée par la courbe noire ou grise.
- Ce sont bien les termes 1, 2, 3, 5, 8… de la suite de Fibonacci qui interviennent le plus souvent dans les indices de phyllotaxie. Cependant les professeurs J.-E. Loiseau et R. V. Jean indiquent que l’on peut aussi rencontrer des indices associés à d’autres suites récurrentes linéaires d’ordre deux, définies comme la suite de Fibonacci mais avec des premiers termes différents : 1, 3, 4, 7, 11… (suite de Lucas), ou encore 1, 4, 5, 9… (page 50), ou encore 2, 5, 7, 12… ou encore 1, 6, 7, 13… ou encore 1, 8, 9, 17… Nous avons vu que, a priori, la prise en compte d’un plus grand nombre d’organes, lorsqu’elle est possible, peut permettre de se ramener à la suite de Fibonacci, qui est seulement la plus simple de toutes ces suites. Noter que le nombre de parastiches (h) et le nombre de parastiche (a-h) des espèces de Mammillaria des figures 127 et 128 ne sont pas des termes de la suite de Fibonacci, mais de deux suites de même définition récurrente un+2 = un+1 + un, avec comme premiers termes respectifs u0 = 2 et u1 = 8 pour la première, w0 = 2 et w1 = 4 pour la seconde. D’après les propriétés vues aux pages 16 à 19, ces exceptions restent liées au nombre d’or, donc à l’angle d’or.
- Dans les équations des spirales 1 à 5, les exposants t/20, t/40, t/80, t/120 et t/240 ont été choisis arbitrairement, après quelques tâtonnements. Il reste à savoir comment fixer précisément ces paramètres pour obtenir tel ou tel nombre de parastiche (h) et (a-h), et tel ou tel indice de phyllotaxie.
- Les spirales données dans les ouvrages de Bell & Bryan (1991) et de Loiseau (1969) ne sont pas des spirales logarithmiques/exponentielles : pour le premier, ce sont des spirales du nombre d’or, pour le second, des spirales d’Archimède et parfois des cercles concentriques. En page 14, nous avons vu que la spirale du rectangle d’or est une bonne approximation de l’unique spirale exponentielle d’équation r = e0,30635t. Sachant que la spirale du rectangle d’or est unique à un changement d’échelle près et compte tenu des résultats obtenus sur les figures 76 à 88, la spirale du rectangle d’or ne permet pas, à elle seule, de modéliser toutes les configurations associées aux différents indices de phyllotaxie.
- La « simplicité » qui se cache derrière ces modélisations est toute relative lorsqu’on n’est pas mathématicien-ne, et elle ne devient évidente qu’une fois les pièces du puzzle assemblées.
Plusieurs siècles ont été nécessaires pour découvrir indépendamment le nombre d’or, la suite de Fibonacci, les spirales exponentielles, l’angle d’or et leurs étonnantes propriétés mathématiques, puis pour trouver les relations qui les relient les unes aux autres.
Les exemples de ce type ne manquent pas dans l’histoire des mathématiques : de nombreuses découvertes, initialement sans applications pratiques, se sont révélées par la suite très utiles pour modéliser, parfois de manière inattendue, des phénomènes naturels jusque-là inexpliqués, ou précédemment interprétés ou modélisés de manière moins convaincante. C’est ainsi que des propriétés arithmétiques connues des mathématiciens grecs ont trouvé des applications dans le traitement informatique (théorie des congruences pour la clé de vérification du numéro INSEE utilisé par l’Assurance maladie) et la sécurisation des données (décomposition d’un nombre en facteurs premiers pour le chiffrement RSA). Pendant des siècles, ces propriétés n’avaient été étudiées que pour l’élégance des raisonnements, la formation à la logique, la compétition pour résoudre des problèmes difficiles mais aux énoncés compréhensibles de tous.
- On peut aussi évoquer la « déraisonnable efficacité des mathématiques », que l’on ne sait pas vraiment justifier. Purs produits de la pensée humaine, les mathématiques nous permettent d’expliquer et de modéliser de nombreux phénomènes naturels, aussi bien en astronomie qu’en physique, en chimie, en biologie. Cette étonnante efficacité ne pourrait-elle pas s’expliquer par le fait que notre cerveau fonctionne selon les mêmes règles élémentaires que les phénomènes naturels que nous essayons d’expliquer ?
13.2 Autres phyllotaxies alternes-spiralées
Dans les figures 89 à 95, la spirale générative a été tracée avant de placer les primordia, représentés par des points verts.
Dans ce qui précède, nous avons modélisé uniquement la phyllotaxie alterne spiralée standard, conduisant aux indices de phyllotaxie 5/13, 8/21, 13/34, 21/55, 34/89, 55/144. Les dénominateurs de ces indices n’étant pas des diviseurs entiers de 360, aucun alignement radial ne pouvait apparaître dans la répartition des organes. Ce n’est pas le cas pour les phyllotaxies d’indices 1/1, 1/2, 1/3, 2/5, 3/8, qui peuvent être considérées comme des versions simplifiées de la phyllotaxie alterne spiralée et qui conduisent à des alignements radiaux, appelés orthostiches.
Ces phyllotaxies ne s’observent habituellement pas sur les rosettes de feuilles basales ou sur les capitules : comme précisé aux pages 62 et 63, leurs feuilles ou leurs fleurons n’occuperaient pas au mieux l’espace disponible.
Les angles de divergence de ces phyllotaxies particulières (respectivement égaux à 360°, 180°, 120°, 144°, 135°) sont des approximations rationnelles de l’angle d’or, alternativement par excès et par défaut (tableau 3, page 19).
13.2.1 Phyllotaxie alterne monostique
Les feuilles se répartissent sur une seule orthostiche unilatérale. L’angle de divergence mesure 360°. Cette phyllotaxie s’observe rarement. Chez Phragmites australis (figure 34), aussi bien que chez Eucalyptus globulus) (figures 65 et 66), cette phyllotaxie n’est pas la règle et s’observe uniquement sur des tiges ou des rameaux en recherche de lumière (penchés, horizontaux ou pendants) et potentiellement sous l’action conjointe de la gravité. On passe de la feuille A à la feuille B en parcourant une spire (figure 89, spirale générative non représentée) et un entrenœud : l’indice de phyllotaxie est égal à 1.
13.2.2 Phyllotaxie alterne distique
Les feuilles se répartissent sur deux orthostiches, opposées par rapport à l’axe de la tige. L’angle de divergence mesure 180°. Cette phyllotaxie est fréquente chez les Poacées : Poa compressa (figure 35 à droite), Lolium perenne (figure 38), Arundo donax (figure 36, à droite), espèces à croissance rapide et aux entrenœuds longs et réguliers. Elle s’observe aussi chez d’autres monocotylédones : Allium polyanthum (figure 35 à gauche), inflorescences de Polygonatum multiflorum (figure 36, à gauche), plus rarement chez certaines dicotylédones, par exemple sur les jeunes rameaux horizontaux ou pendants de tilleul ou d’orme lisse (figure 37) ou de Diospyros lotus (figure 64). On passe de la feuille A à la feuille C en parcourant une spire (figure 90, spirale générative non tracée) et deux entre-nœuds : l’indice de phyllotaxie est égal à 1/2.
13.2.3 Phyllotaxie alterne tristique
Les feuilles se répartissent sur trois orthostiches (figure 91). L’angle de divergence mesure 120°. Cette phyllotaxie s’observe sur les Cypéracées, comme Carex pendula (figure 39). On passe de la feuille A à la feuille D en parcourant une spire et trois entrenœuds : l’indice de phyllotaxie est égal à 1/3.
13.2.4 Phyllotaxie alterne pentastique
Les feuilles se répartissent sur cinq orthostiches disposées en étoile (figure 92). L’angle de divergence mesure 144°. Cette phyllotaxie exceptionnelle s’observe sur les tiges d’Aloe juvenna (figure 40). On passe de la feuille A à la feuille F en parcourant deux spires et cinq entre nœuds : l’indice de phyllotaxie est égal à 2/5.
Sur la figure 92, en plus des cinq orthostiches (un point toutes les deux spires), on distingue (figure 93) :
- huit parastiches (a-h), matérialisées par les courbes vertes (un point à toutes les trois spires),
- cinq parastiches (h), matérialisées par les courbes rouges (un point à toutes les trois spires).
13.3.5 Phyllotaxie alterne octostique
L’angle de divergence mesure 135°. Les feuilles se répartissent sur huit orthostiches disposées en étoile et deux par deux opposées dans quatre plans faisant entre eux des angles de 45° (figure 94). Cette phyllotaxie exceptionnelle s’observe sur Euphorbia obesa (figure 41) et sur la Cactacée Astrophytum asterias (espèce non représentée). On passe de la feuille A à la feuille I en parcourant trois spires et huit entrenœuds : l’indice de phyllotaxie est égal à 3/8.
Sur la figure 94, en plus des huit orthostiches (un point toutes les trois spires), on distingue (figure 95) :
- trois parastiches (a-h), matérialisées par les courbes rouges (un point à chaque spire),
- cinq parastiches (h), matérialisées par les courbes vertes (un point toutes les deux spires).
13.3. Phyllotaxies opposées : deux feuilles par nœud
Les phyllotaxies opposées sont caractérisées par une alternance d’un entrenœud long avec un entrenœud nul ou très court, ce qui conduit à la formation simultanée ou quasi simultanée de paires d’organes, opposés l’un à l’autre de part et d’autre du nœud de la tige.
13.3.1 Phyllotaxie opposée distique
Les feuilles sont opposées par paires et disposées sur deux demi-droites opposées, de part et d’autre de la tige (figure 96). Entre les feuilles d’une même paire, l’angle de divergence est de 180°.
13.3.2 Phyllotaxie opposée décussée
Les feuilles sont opposées par paires. Entre deux feuilles d’une même paire, l’angle de divergence est de 180°, mais deux paires consécutives sont décalées de 90° (figure 97). Cette phyllotaxie est celle des Lamiacées (figure 43, à droite), aux tiges le plus souvent quadrangulaires. C’est aussi celle des pièces florales de Papaver rhoeas (figure 46).
13.3.3 Phyllotaxie multijuguée
Les feuilles sont opposées par paires. Entre deux feuilles d’une même paire, l’angle de divergence est de 180°, mais deux paires consécutives sont décalées de 68,75° (moitié de la mesure de l’angle d’or). Cette phyllotaxie, modélisée sur la figure 98, s’observe chez Vinca major (figure 47) et chez Mercurialis perennis (figure 48).
13.4. Phyllotaxies verticillées : au moins trois feuilles par nœud
Les phyllotaxies verticillées sont caractérisées par une alternance d’au moins deux entrenœuds très courts ou nuls, avec un entrenœud long, ce qui est assimilable à la formation simultanée ou quasi simultanée de verticilles d’au moins trois organes, séparés des verticilles voisins par un entrenœud long (très court ou nul lorsqu’il s’agit de pièces florales).
13.4.1 Trois feuilles par nœud : phyllotaxie verticillée tristique
Les feuilles (ou les pièces florales) sont verticillées par trois. Entre les feuilles ou les pièces florales d’un même verticille, l’angle de divergence est de 120°, mais deux verticilles consécutifs sont décalés de 60° (figure 99). Cette phyllotaxie s’observe par exemple chez Juniperus communis (figure 49 à gauche), chez certaines bruyères (figure 49 à droite), chez Nerium oleander (figure 50). Elle est habituelle sur les pièces florales des Monocotylédones (figure 51).
13.4.2 Quatre feuilles par nœud : phyllotaxie ventriculée, ou verticillée tétrastique
Les feuilles sont verticillées par quatre. Entre les feuilles ou les pièces florales d’un même verticille, l’angle de divergence est de 90°, mais deux verticilles successifs sont décalés de 45° (figure 100). Cette phyllotaxie s’observe rarement sur les feuilles, par exemple chez Sedum cepaea (figure 52), chez Pedicularis verticillata (figure 54), chez la Erica tetralix (non illustrée) ou encore, très exceptionnellement, chez Nerium oleander (figure 50). Elle s’observe bien plus souvent sur les fleurs, car plusieurs familles de plantes (Brassicacées, Onagracées, Ericacées, etc.) présentent – ou peuvent présenter – des fleurs tétramères (figures 55, 56 et 57).
13.4.3 Cinq feuilles par nœud : phyllotaxie verticillée pentastique
Les feuilles ou les pièces florales sont verticillées par cinq. Entre les feuilles ou les pièces florales d’un même verticille, l’angle de divergence est de 72°, mais deux verticilles successifs sont décalés de 36° (figure 101). Sur les feuilles, cette phyllotaxie ne s’observe guère que chez les myriophylles (non illustrés), mais elle est très fréquente, en verticilles bien distincts, sur les pièces florales de très nombreuses Dicotylédones (figures 58 et 59).
13.4.4 Six feuilles par nœud : phyllotaxie verticillée hexastique
Les feuilles ou les pièces florales sont verticillées par six. Entre les feuilles de chaque verticille, l’angle de divergence est de 60°, mais deux verticilles successifs sont décalés de 30° (figure 102). Cette rare phyllotaxie s’observe chez Polygonatum verticillatum (figure 60, à droite).
14. Croissance des végétaux et phyllotaxie. Illustrations de la phyllotaxie alterne spiralée standard
14.1. Les capitules des Asteracées
Un capitule est une inflorescence résultant du raccourcissement extrême d’un axe floral portant de nombreux fleurons (fleurs sans pédicelle), groupés sur un réceptacle habituellement en forme de disque et entouré d’un involucre de bractées, parfois épineuses.
Sur les capitules des Astéracées, aux fleurons nombreux, la spirale générative ne se perçoit pas. Seules les parastiches formées par les bractées de l’involucre et celles formées par les fleurons sont habituellement visibles, du moins lorsque les corolles sont tubulaires, avec des pétales à parties libres courtes et triangulaires.
Le nombre des parastiches qui s’enroulent dans le sens horaire (h) et le nombre des parastiches qui s’enroulent dans le sens anti-horaire (a-h) sont a priori deux termes consécutifs de la suite de Fibonacci. Chez Silybum marianum (figure 103), tous les fleurons sont tubulaires mais, comme chez l’artichaut, les parties libres des pétales sont filiformes : les parastiches formées par les fleurons ne sont visibles que si l’on coupe le capitule (figure 113) ; les parastiches formées par les bractées de l’involucre sont plus visibles, mais bien moins nombreuses que celles que forment les fleurons.
Chez Bellis perennis (figure 104), les Leucanthemum (figure 105) et Pallenis spinosa (figure 106), seules les nombreuses petites fleurs tubulées centrales du capitule sont fertiles ; elles sont entourées de grandes fleurs stériles en languettes, le tout simulant une très grande fleur, visible de loin par les pollinisateurs.
Chez Helianthus (figures 107 à 110), lorsque les premières fleurs formées (celles qui sont en périphérie du capitule) commencent à fleurir, les parastiches sont à la fois nombreuses et régulières ; en fin de développement, et vers le centre, les parastiches deviennent moins nombreuses, se brouillent puis disparaissent.
Chez les Carlina (figures 111 et 112), les paillettes qui entourent chaque fleuron restent solidement soudées entre elles, en un disque légèrement bombé qui se détache du capitule en automne ou au cours de l’hiver. Emporté par le vent avec les akènes qu’il contient encore, ce disque de paillettes reste intact pendant au moins un an. Les photos montrent de tels disques, vus de dessous.
Pour observer les parastiches sur un capitule d’artichaut cru (figure 113), enlever les bractées de l’involucre, couper le « foin » (fleurons + paillettes) à sa base, avec un couteau bien affûté, en un seul mouvement.
Chez Urospermum dalechampii (figure 114) et les Taraxacum (figures 115 à 117) ou d’autres espèces aux fleurs toutes fertiles et ligulées, les parastiches sont visibles sur les fleurons centraux non encore épanouis (mais pas sur le capitule épanoui, qui simule une unique fleur jaune de grand diamètre), puis se retrouvent sur le réceptacle lorsque les akènes se détachent à maturité. Entretemps, celui-ci est devenu plus ou moins sphérique (figures 116 et 117), ce qui permet aux akènes de se développer (puis d’être dispersés par le vent) sans que leurs aigrettes de poils plumeux ne soient entremêlées.
Chez Echinops ritro (figure 118), le réceptacle, sphérique dès le début, est un capitule de capitules uniflores.
Chez l’Edelweiss (Leontopodium nivale subsp. alpinum, figure 119), l’inflorescence est un capitule de capitules.
14.2. Autres exemples
La phyllotaxie alterne spiralée standard se retrouve chez de nombreuses autres plantes : inflorescence du chou romanesco (figure 120), qui donne un bel exemple de motif fractal, ombelles d’ombellules de la carotte sauvage (figure 121), ananas (figure 122), cônes de pin (figure 123), cupules des glands du chêne kermès (figure 124), capitule ovoïde de cardère (figure 125), etc.
Les parastiches, fréquentes chez les plantes des déserts, s’observent sur les feuilles des espèces aux tiges fortement raccourcies des Agavacées (figure 126), mais aussi des Xanthorrhoeacées sud-africains (Aloe perfoliata, figure 25) et des Didiereacées malgaches (non représentées).
Elles s’observent aussi sur les tiges renflées (et parfois ramifiées) de nombreuses Cactacées, de forme souvent oblongue, cylindrique, globuleuse ou sphérique (figures 127 à 130). Chez les Cactacées, les nombres de parastiches font parfois exception à l’omniprésence des termes de la suite de Fibonacci, en particulier dans le genre Mammillaria. Sur le spécimen de Mammillaria de la figure 127, on compte 10 parastiches (a-h) et 18 parastiche (h). Ces deux nombres ne sont pas des termes de la suite de Fibonacci, mais probablement les termes u2 et u3 de la suite définie par l’algorithme de Fibonacci, avec comme premiers termes u0 = 2 et u1 = 8 (exception signalée par Loiseau, 1969). Cependant, d’après le résultat prouvé page 17, la phyllotaxie de cette espèce reste liée à l’angle d’or.
D’un point de vue mathématique, la solution proposée ci-dessus n’est pas unique… D’autres suites récurrentes linéaires d’ordre deux pourraient être envisagées, par exemple celle qui est définie par la relation récurrente ![]() avec
avec ![]() et
et ![]() . On retrouve
. On retrouve ![]() et
et ![]() , mais cette solution est peu probable, car elle ferait exception à ce qui semble être une règle générale de la phyllotaxie : cette suite n’est pas liée au nombre d’or, puisque
, mais cette solution est peu probable, car elle ferait exception à ce qui semble être une règle générale de la phyllotaxie : cette suite n’est pas liée au nombre d’or, puisque ![]() .
.
Sur le spécimen de Mammillaria spinosissima de la figure 128, la tige principale porte deux rameaux, sur lesquels on compte sans surprise 5 parastiche (h) et 8 parastiches (a-h). Ces deux nombres sont des termes de la suite de Fibonacci alors que, sur la tige principale, on compte 10 parastiches (a-h) et 16 parastiches (h), qui ne sont pas des termes de cette suite. Ce sont probablement les termes u3 et u4 de la suite définie par l’algorithme de Fibonacci, mais avec comme premiers termes u0 = 2 et u1 = 4. Cette phyllotaxie, variable selon que l’on considère la tige principale ou ses rameaux, reste liée au nombre d’or et à l’angle d’or.
On peut faire des observations comparables sur le célèbre « coussin de belle-mère », Echinocactus grusonii (figure 130).
PARTIE III
Nombre d’or et suite de Fibonacci, de l’Antiquité à nos jours
Il serait difficile de parler du nombre d’or sans aborder le mythe de son utilisation en architecture et dans les arts depuis la plus haute antiquité.
15. Quelques dates
La figure 131 propose une chronologie simplifiée, utile à la compréhension de ce qui suit.
16. Le nombre d’or dans l’Antiquité
16.1 Les instruments de mesure
16.1.1 Le cordeau, instrument universel de l’arpenteur et de l’architecte
Le cordeau est une fine cordelette – aussi peu élastique que possible – que l’on tient tendue entre ses extrémités pour matérialiser un segment de ligne droite. Avant d’être un outil de jardinage, le cordeau a été le premier instrument d’arpentage : maintenu à tension constante, il permet aussi bien de mesurer ou de reporter rapidement des distances que de tracer au sol des cercles de centre et de rayon donnés, ou encore des ellipses (figure 132) plus ou moins aplaties, le tout avec une précision raisonnable, sachant que la longueur d’un cordeau en fibres végétales dépend de sa tension et de son degré d’humidité.
Pour tracer une ellipse avec un cordeau :
- faire une boucle qui entoure deux piquets fixes, plantés dans le sol en A et en B,
- tendre le cordeau avec une pointe M, puis déplacer M en gardant la boucle bien tendue.
La longueur AM + MB étant constante, M décrit une ellipse de foyers A et B. L’ellipse s’arrondit lorsqu’on rapproche A et B l’un de l’autre (c’est un cercle lorsque A et B sont confondus) et s’aplatit lorsqu’on les éloigne.
Pour mesurer de courtes distances de manière plus précise, les bâtisseurs utilisaient une règle graduée. La règle, l’équerre et le compas à deux branches articulées étaient utilisés au Moyen-Orient (Mésopotamie, Égypte et Grèce) depuis la plus haute Antiquité, mais ces instruments sont de trop petite taille pour être utilisés sur le terrain. Le plus ancien compas, trouvé en Égypte, est daté du xiie siècle av. J.-C. Après avoir aménagé une aire bien plane, pouvant ensuite servir de parvis si elle avait été dallée, les architectes traçaient au sol, en grandeur réelle, les plans des murs et des façades. Ils utilisaient pour cela le cordeau et divers instruments de visée. Pour tracer au sol une ligne droite, il suffit d’enduire un cordeau de poussière de craie ou de poudre colorée, de le tendre, de le pincer en son milieu en le tirant vers le haut, puis de le relâcher. Le trait peut ensuite être matérialisé de manière plus pérenne, par exemple en le gravant sur un dallage plan. Une fois le plan tracé, les pierres taillées étaient ajustées au sol et à plat, numérotées, avant d’être assemblées verticalement lors de la construction des murs.
Plus récemment, lors de la construction du viaduc du Viaur (achevé en 1902) sur la voie ferrée entre Albi et Rodez, les poutres en treillis métalliques ont été assemblées (avec des rivets frappés à chaud, comme pour la tour Eiffel) en gros modules, puis ces modules ont été provisoirement pré-assemblés entre eux sur un terrain aplani proche du futur viaduc. Ils ont ensuite été désassemblés, puis transportés sur le chantier de construction pour assemblage définitif.
Pour contrôler la verticalité, les bâtisseurs de l’Antiquité utilisaient le fil à plomb. Pour contrôler l’horizontalité et les alignements, les Grecs utilisaient la « dioptra » et le niveau de maçon. Chacun de ces deux instruments est constitué d’un triangle rectangle isocèle et d’un fil à plomb, matérialisé, sur la figure 133, par une flèche rouge indiquant la direction verticale :
- à gauche, sur la dioptra, le fil à plomb est suspendu au milieu I de l’hypoténuse [AB] et l’instrument est tenu pointe de l’angle droit tournée vers le bas : l’hypoténuse, qui sert d’axe de visée, est horizontale lorsque le fil à plomb passe par le sommet C de l’angle droit ;
- à droite, sur le niveau de maçon, le fil à plomb est suspendu au sommet F de l’angle droit et l’instrument est tenu pointe de l’angle droit tournée vers le haut : lorsque le fil à plomb passe par le milieu J de l’hypoténuse [DE], cette dernière est horizontale.
Par la suite, dans la dioptra, le triangle a été remplacé par un demi-cercle gradué, permettant de mesurer l’angle de l’axe de visée (AB) par rapport à l’horizontale, et plus tard encore complété par un disque permettant de mesurer des angles dans le plan horizontal.
Les premiers instruments de topographie moderne, apparus au xvie siècle, sont issus de la dioptra. Les théodolites actuels, qui permettent de mesurer des angles avec une très grande précision, reposent sur le même principe de base.
Entre 1792 et 1798, les astronomes Delambre et Méchain ont pu déterminer, avec une bonne précision, la longueur d’un arc du méridien de Paris, entre Dunkerque et Barcelone : Delambre entre Dunkerque et Rodez, Méchain entre Barcelone et Rodez. Ce difficile travail avait pour but de définir la longueur du mètre étalon, dix-millionième partie d’un quart de méridien terrestre. C’est pour cela que le diamètre de la Terre, supposée sphérique, était théoriquement égal à 40 000 km. Dans les monts de Lacaune, au sommet du Montalet (1 259 m d’altitude), on peut voir l’une des bornes de triangulation qui ont servi à Méchain lors de son passage dans le Tarn.
16.1.2 La corde à treize nœuds et le théorème de Pythagore
Pour mesurer ou reporter des distances exprimées dans une unité de longueur donnée, il suffit de faire des nœuds régulièrement espacés sur un cordeau.
Dans l’Antiquité, deux nœuds successifs étaient habituellement espacés entre eux d’une coudée. Les coudées antiques, longueurs entre le coude et le bout du majeur, mesuraient environ 50 cm, mais leur longueur précise était variable selon le lieu et l’époque. Des cordes à nœuds (ou des chaînes de plantation) sont toujours utilisées par les jardiniers pour planter des végétaux à intervalles réguliers.
Cependant, une corde à nœuds ne permet que des mesures approximatives. Pour des mesures d’arpentage plus précises, on utilisait jusqu’à une époque récente une chaîne d’arpenteur à maillons métalliques, insensible à l’humidité et de longueur constante à tension et à température données. Pour des mesures précises, on effectuait une correction pour tenir compte de la dilatation du métal, fonction de la température.
La corde à treize nœuds était connue des arpenteurs et des architectes sumériens et égyptiens, qui l’utilisaient il y a plus de 4 500 ans. Les treize nœuds délimitent douze intervalles de même longueur. D’une part 3 + 4 + 5 = 12 et d’autre part (3 ; 4 ; 5) est un triplet pythagoricien puisque 3² + 4² = 5². Une unité étant choisie, la réciproque du théorème de Pythagore permet d’affirmer que le triangle de côtés 3, 4 et 5 est rectangle (figure 134).
Cette propriété est connue depuis des millénaires : la tablette « Plimpton 322 », trouvée vers 1920 en Irak lors de fouilles illégales, donne une quinzaine de triplets pythagoriciens, dont évidemment le triplet (3 ; 4 ; 5), le plus simple de tous. Certains n’y voient que de simples exercices de calcul, mais cette tablette, probablement écrite en 1 800 av. J.-C., permet de penser que les Sumériens connaissaient depuis longtemps, mais seulement de manière empirique, le fameux théorème démontré par Pythagore 1 200 ans plus tard, aux environs de 600 av. J.-C.
Des textes indiens, datés entre 800 et 500 avant notre ère et connus sous le nom de Sulba-Sutras (littéralement « règles de la corde »), donnent des formulaires contenant des triplets pythagoriciens et de nombreuses constructions de figures géométriques à l’aide de cordes et de piquets. Ces connaissances ont été consignées par différents auteurs, le plus connu étant le mathématicien indien Katyayana, au iie siècle av. J.-C. (consulter l’article Sulba-Sutras sur Wikipédia).
La corde à treize nœuds permet, sans autre outil, sans connaissances géométriques particulières et surtout sans calculs, de tracer un triangle rectangle, donc de matérialiser un angle droit, et de construire diverses autres figures simples, par exemple un triangle équilatéral.
En Occident, la corde à treize nœuds a connu son âge d’or lors de la construction des cathédrales, entre le xe et le xiiie siècle. Dans l’Yonne, aux sud-ouest d’Auxerre, le chantier de construction du château de Guédelon a débuté en 1997 et devrait s’achever en 2025. Les initiateurs de ce projet souhaitent utiliser, valider ou tenter de retrouver expérimentalement les méthodes de construction médiévales du xiiie siècle, en partie oubliées. Dans un chantier ouvert au public, les bâtisseurs de Guédelon n’utilisent que des matériaux de construction disponibles sur place et des outils qu’ils fabriquent eux-mêmes. Leurs instruments de mesure et de traçage sont ceux des bâtisseurs du Moyen Âge : cordeau, corde à treize nœuds, compas, équerre et pige. Cette dernière est un bâton normalisé subdivisé en paume, palme, empan, pied et coudée (pages 81 et 82).
16.2. Le nombre d’or et les bâtisseurs antiques
Dans l’Antiquité, le rectangle d’or, facile à construire au sol avec un cordeau par la méthode de la figure 5, aurait pu servir de format de rectangle pour l’architecture. Mais il semble que cela n’ait pas été le cas : aucune source antique ne permet de prouver que les connaissances sur le nombre d’or et les notions qui lui sont liées aient été diffusées hors du cercle des philosophes mathématiciens de l’école de Pythagore et qu’elles aient été utilisées en architecture. N’en déplaise à ceux qui voient le nombre d’or partout, et qui le « prouvent » en mesurant les monuments de manière adéquate et approximative, alors que les textes antiques qui nous sont parvenus sont tous muets à ce sujet…
Rappelons que, dans la Grèce antique, les philosophes expliquaient le monde à l’aide de nombres entiers et de leurs rapports simples, et qu’ils avaient été profondément désorientés lorsqu’ils ont démontré que la mesure de la diagonale du carré et le nombre d’or étaient des nombres irrationnels. Le nombre d’or et les notions qui lui sont liées avaient alors le même statut que, de nos jours, la théorie de la relativité d’Einstein. Peu de personnes étaient à même de comprendre ces nouvelles notions mathématiques, qui, tout comme la théorie de la relativité depuis une centaine d’années, remettaient en cause une interprétation précédente de l’Univers et amenaient à faire de nouvelles conjectures sur ses origines.
Les bâtisseurs de l’antiquité ne manipulaient a priori que des nombres entiers. Il est bien plus vraisemblable que, lorsqu’une mesure faite a posteriori peut laisser penser qu’ils ont utilisé le nombre d’or, ils aient utilisé un format rationnel (par exemple 8/5 ou d’autres formats proches, comme 5/3 ou 13/8) plutôt que celui du rectangle d’or.
Le rapport 8/5 (de valeur exacte 1,6), le rapport 5/3 (de valeur approchée 1,667) ou encore le rapport 13/8 (de valeur exacte 1,625) diffèrent peu de la valeur approchée 1,618 du nombre d’or. En effet, les nombres 5 et 8, de même que 3 et 5 puis 8 et 13, sont des termes consécutifs de la suite de Fibonacci. De plus, la corde à treize nœuds ne permet pas une construction immédiate du rectangle d’or (figure 142), alors qu’elle donne une construction immédiate de rectangles aux formats 8/5 (figure 143), 5/3 et 13/8.
La figure 135 permet de comparer visuellement un rectangle d’or et un rectangle de format 8/5 et de même aire. Tout est dans l’épaisseur des traits ! Verriez-vous la différence entre les deux formats si les traits du dessin étaient plus épais ? Ou si ces rectangles étaient l’un à côté de l’autre ? Ou s’ils étaient différemment orientés ? Ou encore s’ils étaient de tailles différentes ? Un bon dessin vaut mieux qu’un long discours…
Pour construire la figure 135, considérons un rectangle ABCD de format 8/5. Si, dans le rectangle AEFG, nous posons AG = x alors x sera la solution positive de ![]() . Alors AG » 4,972 m et AE » 8,045 m. Pour chacune de ces deux mesures, l’écart avec les mesures correspondantes de ABCD n’est que d’environ 0,56 %. Lorsqu’on sait que 5 et 8 sont deux termes consécutifs de la suite de Fibonacci, il n’y a pas lieu d’être surpris que ces deux rectangles soient de dimensions aussi voisines.
. Alors AG » 4,972 m et AE » 8,045 m. Pour chacune de ces deux mesures, l’écart avec les mesures correspondantes de ABCD n’est que d’environ 0,56 %. Lorsqu’on sait que 5 et 8 sont deux termes consécutifs de la suite de Fibonacci, il n’y a pas lieu d’être surpris que ces deux rectangles soient de dimensions aussi voisines.
Chacun comprendra qu’aucune mesure effectuée sur un bâtiment ancien ne permet d’affirmer que son concepteur a sciemment utilisé le nombre d’or pour en déterminer les proportions, sauf s’il en existe des preuves historiquement indiscutables. Depuis l’engouement suscité par le nombre d’or au xixe siècle, les deux monuments le plus souvent cités comme étant construits dans les proportions du nombre d’or sont la pyramide de Khéops et le Parthénon d’Athènes.
16.3. La pyramide de Khéops
Les seules données fiables que nous ayons sur la pyramide de Khéops sont au nombre de trois :
- ses dimensions initiales (estimées) et ses dimensions actuelles, sachant que son revêtement de calcaire blanc et lisse a disparu ;
- la relation, citée par Hérodote, qui a vécu entre 480 et 425 av. J.-C., entre l’aire d’une face latérale et celle du carré construit sur la hauteur ;
- le traité De la mesure du cercle que nous a laissé Archimède, qui a vécu de 287 av. J.-C. à 212 av. J.-C.
Rappelons que, au moment de la construction de la pyramide de Khéops (environ 2 500 ans av. J.-C.), les mathématiciens de l’Égypte antique ne connaissaient que les nombres entiers naturels (sans le zéro) et leurs fractions simples. Pour effectuer des calculs sur ces fractions, ils les décomposaient en « fractions égyptiennes », en les exprimant comme sommes de fractions de numérateur un et de dénominateur entier.
Par exemple, mais voir compléments dans le glossaire : 2/3 = 1/3 + 1/3 = 1/3 + 1/4 + 1/12.
Le papyrus Rhind (1 650 av. J.-C.), qui reprend des papyrus bien plus anciens, contient des exemples de telles décompositions, ainsi qu’une tentative de quadrature du cercle : « l’aire du cercle de diamètre 9 coudées est celle du carré de côté 8 coudées », ce qui conduit à une valeur de π égale à (16/9)², de valeur décimale approchée 3,1605. La différence avec π est voisine de 0,02.
16.3.1 Dimensions de la pyramide
La pyramide de Khéops, édifiée il y a environ 4 500 ans, est une pyramide régulière de base carrée. Il est admis que le côté a de la base mesurait 440 coudées royales anciennes et que la hauteur h mesurait 280 coudées royales anciennes. À l’origine, les faces de la pyramide portaient un revêtement de calcaire blanc, dont les pierres taillées ont été réutilisées localement pour d’autres constructions. Il manque actuellement ce revêtement et le sommet de la pyramide.
Sous le règne du pharaon Ahmôsis II, qui régna de 571 av. J.-C. à 526 av. J.-C., la hauteur de la pyramide de Khéops n’était semble-t-il pas connue, ou avait été oubliée. Le pharaon lança un défi à qui pourrait la mesurer. C’est Thalès de Milet (de 625 av. J.-C. à 547 av. J.-C.) qui releva le défi et le réussit, en utilisant le théorème sur les droites parallèles qui porte son nom (mais dont il n’est pas l’auteur) et en comparant la longueur de l’ombre de la pyramide avec celle d’un bâton vertical. À cette date, le théorème de Thalès n’était connu que de manière empirique : sa démonstration a été faite par Euclide dans ses Éléments, plus de 200 ans plus tard.
Selon les sources, la coudée royale ancienne – divisée en sept « paumes » et vingt-huit « doigts » – mesurait environ 52,35 cm, mais sa mesure exacte semble avoir changé au cours des siècles. Cette coudée royale étant utilisée en architecture, il n’est pas surprenant que la hauteur de la pyramide de Khéops soit un multiple de sept. N’oublions pas que, comme dans le reste du monde antique moyen-oriental, les Égyptiens privilégiaient les nombres entiers et leurs rapports simples et que sept était un nombre divin.
Pour cette valeur de la coudée royale ancienne, le côté a devrait mesurer 230,34 m. Sa mesure actuelle donne en moyenne 230,36 m. Remarquable précision, mais la valeur de la coudée qui nous sert de référence a peut-être été déterminée à partir de mesures effectuées sur la pyramide… au xixe siècle ou au xxe siècle. Quoi qu’il en soit, la construction a été réalisée avec une grande précision : pour chacun des quatre côtés de la base, l’écart à cette moyenne est moindre que 11 cm ! La figure 136 représente une pyramide régulière de hauteur h et de base carrée de côté a = 440 et de hauteur h = 280. Sur cette pyramide, il est immédiat que b = 220 coudées royales anciennes et que la pente des faces triangulaires, par définition égale à ![]() , est égale à h/b, soit 280/220 ou, après simplification, 14/11. Ceci permettait une taille normalisée précise des pierres du revêtement initial, illustrée sur la figure 137.
, est égale à h/b, soit 280/220 ou, après simplification, 14/11. Ceci permettait une taille normalisée précise des pierres du revêtement initial, illustrée sur la figure 137.
16.3.2 Première série de calculs : calcul du quotient 2a/h et du quotient c/b
Le rapport du côté de la base à la hauteur est ![]() . On remarquera que 2a/h est égal à 22/7, résultat donné par le calcul de la deuxième réduite du développement en fraction continue du nombre π (voir page 5). Au millionième près le plus proche, 22/7 = 3,142857 et π = 3,141593. L’écart entre ces deux valeurs est à peine supérieur à 0,001.
. On remarquera que 2a/h est égal à 22/7, résultat donné par le calcul de la deuxième réduite du développement en fraction continue du nombre π (voir page 5). Au millionième près le plus proche, 22/7 = 3,142857 et π = 3,141593. L’écart entre ces deux valeurs est à peine supérieur à 0,001.
Sur la figure 136, le triangle EFG est rectangle en E. D’après le théorème de Pythagore, c² = b² + h². Pour a = 440 et h = 280 on obtient c² = 220² + 280² = 126800, donc ![]() , d’où c/b ≈ 1,618590. La valeur approchée de φ, au millionième le plus proche, est égale à 1,618034 : l’écart entre la valeur de φ et celle de c/b est inférieur à 0,001.
, d’où c/b ≈ 1,618590. La valeur approchée de φ, au millionième le plus proche, est égale à 1,618034 : l’écart entre la valeur de φ et celle de c/b est inférieur à 0,001.
Pour de nombreux amateurs d’ésotérisme, ce résultat est suffisant pour affirmer que le « secret de la pyramide de Khéops » (à supposer qu’il y en ait un) réside dans la présence du nombre d’or, qui aurait été utilisé pour déterminer, de manière cryptée, les dimensions de l’édifice.
16.3.3 Le traité d’Archimède
Au moment de la construction de la pyramide de Khéops, les savants égyptiens savaient-ils que c’est le même nombre (actuellement appelé π ou « constante d’Archimède ») qui intervient simultanément dans le calcul du périmètre d’un cercle de rayon R, égal à 2πR, et dans le calcul de l’aire du disque de rayon R, égale à π = πR² ? On peut en douter : les textes anciens font uniquement référence, pour ce dernier calcul, à des comparaisons entre l’aire d’un disque et celle d’un carré, dans le but de trouver une quadrature du cercle (voir complément dans le glossaire).
C’est à Archimède (287 av. J.-C. à 212 av. J.-C.) que l’on doit la preuve que c’est bien le même nombre qui relie le diamètre (ou le rayon) d’un cercle à la fois à son périmètre et à son aire. Dans son traité De la mesure du cercle, Archimède fait deux propositions :
- 1) l’aire d’un cercle est égale à celle d’un triangle rectangle dont un côté est le rayon du cercle et l’autre côté de l’angle droit à la circonférence du même cercle ;
- 2) un cercle est au carré construit sur son diamètre, à très peu de choses près, comme 11 est à 14.
La proposition 1 indique comment calculer l’aire d’un disque de rayon R :
A = 1/2 x R x 2πR, donc A = π x R².
La proposition 2 demande à être traduite en langage actuel. Nous savons que l’aire d’un cercle de diamètre D est égale à π x D²/4 et que l’aire d’un carré de côté D est égale à D². Après simplification, l’approximation (π x D²/4)/D² ≈ 11/14 donnée par Archimède conduit à π/4 ≈ 11/14, puis à π ≈ 22/7.
N’oublions pas que la corde à nœuds était l’outil de base des arpenteurs géomètres égyptiens, qui redéfinissaient les dimensions des parcelles agricoles après chaque crue du Nil. Sans connaissances mathématiques particulières, en utilisant une simple corde à nœuds et en faisant preuve de curiosité et de persévérance, il est possible et assez facile de constater que le périmètre d’un cercle de diamètre 7 entrenœuds est très voisin de 22 entrenœuds, ce qui revient à considérer que 22/7 est une bonne valeur expérimentale du rapport du périmètre d’un cercle à son diamètre. Effectivement, 22/7 ≈ 3,1428 et 22/7 – π ≈ 0,00126. Autrement dit, en prenant comme valeur de π, le périmètre calculé pour un cercle de diamètre 1 m ne diffère de sa valeur exacte que de 1,26 mm, soit une erreur relative de seulement 0,04 %. Difficile de faire mieux avec une simple corde à nœuds !
Les constructeurs de la pyramide avaient-ils observé cette propriété, qui relie avec une remarquable précision le diamètre d’un cercle à son périmètre ? Aucune preuve historique antérieure au traité d’Archimède n’atteste qu’elle était connue. Cependant, Archimède – comme tous les autres savants de l’Antiquité – n’est pas l’auteur de toutes les connaissances qu’il nous a transmises.
16.3.4 Relation rapportée par Hérodote
Selon l’historien et géographe grec Hérodote, qui aurait obtenu ce renseignement auprès des grands prêtres égyptiens, « les surfaces latérales triangulaires de la pyramide de Khéops ont une aire égale à celle du carré construit sur la hauteur ».
En prenant une coudée royale au carré comme unité d’aire, l’aire exacte d’une face latérale de la pyramide de Khéops est égale à a x c / 2, de valeur approchée 78 339,77 et celle du carré construit sur la hauteur est égale à 78 400. L’écart entre ces deux valeurs n’est que d’approximativement 60 coudées au carré, soit environ 16,5 m², avec une erreur relative inférieure à 0,1 %. Rien ne dit que la relation rapportée par Hérodote était connue depuis la construction de la pyramide : elle pouvait avoir été expérimentalement vérifiée bien après cette construction, et avec une précision suffisante (difficile à surpasser avec les instruments de mesure et les capacités de calcul de cette époque), pour qu’elle ait pu être considérée comme exacte.
Comment, dans l’Antiquité, pouvait-on comparer l’aire d’un triangle à l’aire d’un carré ? Cette comparaison ne se faisait pas, comme nous le faisons actuellement, par un calcul numérique, mais par une construction géométrique en deux étapes : en comparant l’aire du triangle à celle d’un rectangle (figure 138), puis celle-ci à l’aire d’un carré, par la quadrature du rectangle (figure 139).
Dans les Éléments, son ouvrage fondamental écrit aux environs de 300 av. J.-C., Euclide a réussi à rassembler et à organiser toutes les connaissances mathématiques de son époque, qu’il en soit ou non l’auteur. Il a repris, entre autres, les acquis de l’école de Pythagore (créée en 532 av. J.-C., très active du vivant de son fondateur, mort en 495 av. J.-C.), mais on ne sait pas si la méthode qu’il propose pour la quadrature du rectangle était déjà connue à l’époque d’Hérodote, qui a vécu entre 480 av. J.-C. et 425 av. J.-C.
Pour construire la figure 139 :
- construire un rectangle ABCD, de longueur L et de largeur l ;
- sur la demi-droite [AD], placer le point C’ tel que DC’ = DC ;
- tracer le cercle de centre O, milieu de [AC’] ;
- ce cercle coupe la demi-droite [CD) en G ;
- construire le carré DEFG, de côté m.
Alors m² = L x l, donc m est la moyenne géométrique de L et l (telle que ![]() ) et l’aire du carré DEFG est égale à celle du rectangle ABCD. Prouvez-le ! La quadrature du rectangle n’était probablement pas connue lors de la construction de la pyramide de Khéops (environ 2 500 av. J.-C.) mais elle pouvait l’être à l’époque d’Hérodote (entre 480 et 425 av. J.-C.).
) et l’aire du carré DEFG est égale à celle du rectangle ABCD. Prouvez-le ! La quadrature du rectangle n’était probablement pas connue lors de la construction de la pyramide de Khéops (environ 2 500 av. J.-C.) mais elle pouvait l’être à l’époque d’Hérodote (entre 480 et 425 av. J.-C.).
En supposant l’égalité entre l’aire d’une face latérale et celle du carré construit sur la hauteur, retrouvons-nous la relation c/b ≈ φ ?
En langage mathématique actuel :
- l’aire du carré construit sur la hauteur h de la pyramide est égale à h² et, d’après le théorème de Pythagore, dans le triangle EFG rectangle en E, h² = c² – b² ;
- l’aire du triangle BCF est égale à 1/2 x a x c et, comme 1/2 x a = b, elle est égale à b x c.
Partant des relations h²= c² – b² et h² = b x c on obtient successivement :
c² – b² = b x c
c² – b x c – b² = 0
En divisant les deux membres par b², (c/b)² – c/b – 1 = 0. Nous avons vu, page 4, que la solution positive de cette équation est φ. La relation rapportée par Hérodote conduit à l’égalité c/b = φ.
On peut trouver une autre relation entre φ et les dimensions de la pyramide. De la relation h² = c² – b² et sachant que φ² – 1 = φ, on déduit successivement :
h²/b² = c²/b² – 1
(h/b)² = (c/b)² _ 1
(h/b)² = φ² – 1
Alors (h/b)² = φ et finalement ![]() . On en déduit que
. On en déduit que ![]() , soit environ 279,84 coudées. Cette valeur n’est pas exactement égale à 280 coudées, mais elle n’en diffère que de 0,156 coudée, c’est-à-dire à peine plus de 8 cm, soit de nouveau une erreur relative inférieure à 0,1 %. Une telle différence était difficilement mesurable jusqu’à l’apparition des théodolites modernes.
, soit environ 279,84 coudées. Cette valeur n’est pas exactement égale à 280 coudées, mais elle n’en diffère que de 0,156 coudée, c’est-à-dire à peine plus de 8 cm, soit de nouveau une erreur relative inférieure à 0,1 %. Une telle différence était difficilement mesurable jusqu’à l’apparition des théodolites modernes.
16.3.5 La pyramide de Khéops contiendrait-elle une relation cryptée entre π et φ ?
* Si 2a/h = π , c/b est-il égal à φ ?
Si 2a/h = π, alors h = 2a/π. Sachant que b = a/2 et que c² = b² + h², on obtient successivement :
![]()
Finalement : ![]()
On en déduit que, si 2a/h = π, alors c/b n’est pas exactement égal à φ. Cependant, les deux valeurs sont très voisines puisque c/b – φ ≈ 0,0001.
* Si c/b = φ , 2a/h est-il égal à π ?
De c² = b² + h² et c/b = φ, on déduit successivement :
![]()
De a = 2b et ![]() , on déduit successivement :
, on déduit successivement :
![]()
Finalement ![]() . On en déduit que, si c/b = φ, alors 2a/h n’est pas exactement égal à . Cependant, les deux valeurs sont très voisines puisque 2a/h – π ≈ 0,003. Au final, il n’y a aucune relation exacte entre π et φ dans les dimensions de la pyramide.
. On en déduit que, si c/b = φ, alors 2a/h n’est pas exactement égal à . Cependant, les deux valeurs sont très voisines puisque 2a/h – π ≈ 0,003. Au final, il n’y a aucune relation exacte entre π et φ dans les dimensions de la pyramide.
L’un des nombres π ou φ peut-il avoir été utilisé à dessein pour choisir les dimensions de la pyramide de Khéops ?
16.3.6 La pyramide et le nombre π
Les calculs qui traduisent les propositions 1 et 2 d’Archimède, formulées plus de vingt siècles après la construction de la pyramide de Khéops, et ceux que nous avons faits sur les dimensions de ce monument conduisent aux rapports 11/14 et 22/7. Nous avons vu que, avant la parution du traité d’Archimède, aucun document historique n’indique que le rapport entre le périmètre d’un cercle et son diamètre est « égal » à 22/7 ou proche de cette valeur, mais cette connaissance était probablement antérieure.
Les bâtisseurs de la pyramide avaient-ils cette connaissance ? On ne peut pas l’exclure, mais il n’en existe aucune preuve. Si, depuis la plus haute Antiquité égyptienne, elle était connue et réservée aux seuls initiés, elle a probablement été peu diffusée et les textes qui la mentionnaient (s’il y en a eu) ont dû être rares : ils peuvent avoir été perdus ou sont encore à découvrir.
16.3.7 La pyramide et le nombre φ
Revenons à la relation citée par Hérodote. Les calculs précédents montrent que, dans la pyramide de Khéops, l’égalité entre l’aire d’une face latérale et celle du carré construit sur sa hauteur conduit effectivement à l’égalité c/b = φ. Ces calculs n’étaient a priori pas possibles il y a 4 500 ans.
Rappelons que les rares Égyptiens instruits (prêtres et scribes) ne connaissaient que les nombres entiers et leurs fractions simples, sur lesquelles ils calculaient de manière très particulière. Au moment de la construction de la pyramide, son architecte n’avait a priori aucun outil mathématique lui permettant de sortir de ce cadre de calcul très restreint et de faire des calculs sur des nombres irrationnels, inconcevables à cette époque.
La relation rapportée par Hérodote peut n’avoir été remarquée que bien après la construction de la pyramide et seulement de manière expérimentale, par des mesures d’une précision suffisante pour que l’on ait pu penser qu’elle était vérifiée. Ceci peut-être seulement après le vie siècle av. J.-C., et par exemple (simple conjecture) en comparant des aires sur une maquette et à la suite de la découverte de la quadrature du rectangle par les mathématiciens grecs.
Aucun document historique ne permet d’affirmer que le nombre d’or était connu lors de la construction de la pyramide : il n’a été caractérisé que deux mille ans plus tard, par l’école de Pythagore. Il est donc très probable que les valeurs données à α et à h n’ont pas été choisies à dessein pour obtenir la relation c/b ≈ φ.
16.3.8 Conclusion
Les calculs précédents montrent que, si le choix a = 440 et h = 280 a été fait pour que π apparaisse comme valeur du quotient , on peut aussi croire qu’il a été fait pour que φ apparaisse comme valeur du quotient c/b, et réciproquement.
En appliquant le principe de parcimonie et si l’un ou l’autre des nombres π ou φ a été volontairement caché dans les dimensions et de la pyramide de Khéops (ce qui reste à prouver), il semble plus probable que ce soit le nombre π plutôt que le nombre π. Cependant, ce choix a pu être fait pour une tout autre raison, très éloignée de la volonté de faire apparaître, de manière cryptée, π ou φ dans les dimensions de la pyramide. Il pourrait découler, simple conjecture, du système de mesures utilisé à cette époque : la coudée royale était divisée en 7 paumes de 4 doigts chacune, donc en 28 doigts. En remarquant que 28 = 4 x 7 = 2 x 14, on retrouve 7 et 14, deux des trois nombres qui définissent les rapports 14/11 et 11/7 que nous savons étroitement liés aux dimensions de la pyramide. Resterait à trouver la provenance du nombre 11… Serait-ce simplement parce que 7 + 4 = 11 ?
Cette conjecture est-elle plus invraisemblable que de supposer que π ou φ ont été cachés à dessein dans les dimensions de la pyramide de Khéops ? Il serait intéressant de savoir si les nombres 7, 11 et 14 se retrouvent dans les proportions d’autres monuments contemporains de la construction de la pyramide. Si les valeurs de et de étaient directement liées aux unités de mesure en usage en Égypte il y a environ quarante-cinq siècles, serait-il surprenant, tellement ce choix pouvait leur paraître évident, que les bâtisseurs de la pyramide n’en aient laissé aucune trace ?
Dans ce cas, les relations 2a/h ≈ π et c/b ≈ φ ne seraient que d’étonnantes coïncidences, découvertes a posteriori et plus de quarante siècles après la construction de la pyramide.
Sans traces écrites ou preuves archéologiques, la mémoire collective s’efface rapidement. Nous savons que, du vivant de Thalès, les dimensions de la pyramide n’étaient plus connues. Nous-mêmes ne connaissons qu’une partie des techniques des bâtisseurs du Moyen Âge et, de nos jours, la déclassification de documents jusqu’alors tenus secrets nous éclaire sur des évènements récents dont les derniers témoins viennent juste de disparaître.
Toutes les conjectures, faites au xixe ou au xxe siècle, sur les liens éventuels entre les dimensions de la pyramide de Khéops et les nombres π ou φ, reposent :
- sur les dimensions actuelles de ce monument et sur ses dimensions initiales que l’on ne peut que conjecturer ;
- sur des témoignages recueillis au moins vingt siècles après sa construction ;
- sur des interprétations faites au xixesiècle ou au xxe siècle, qui prêtent aux bâtisseurs de la pyramide des connaissances en mathématiques et des techniques de calcul qui étaient inconnues il y a plus de quatre mille ans. Certaines de ces connaissances, essentiellement géométriques, n’ont été développées que vingt siècles plus tard par Thalès, Pythagore et son école, Hérodote, Euclide, Archimède… D’autres, comme les calculs algébriques, n’ont été développées qu’à partir de la fin du Moyen Âge, et progressivement jusqu’à nos jours.
En attendant des preuves, les archéologues ne disposent d’aucun indice laissé par les constructeurs de la pyramide. Saurons un jour pourquoi les nombres et peuvent être vus dans les dimensions de la pyramide de Khéops ? Le mystère reste entier…
16.4. Le Parthénon
Là aussi, le doute sur l’utilisation du nombre d’or est légitime. Le Parthénon d’Athènes a été construit entre 447 et 432 av. J.-C. À cette époque, la division d’un segment en extrême et moyenne raison et le rectangle d’or étaient connus de l’école pythagoricienne depuis au moins cinquante ans, mais rien n’indique que ces connaissances aient été diffusées hors du cercle fermé des mathématiciens ni qu’elles aient été utilisées en architecture et dans les arts.
Le format du rectangle dans lequel on peut inscrire la façade (toit compris) varie d’environ 1,5 à environ 1,7. Cette fourchette est approximativement centrée sur le nombre d’or (de valeur approchée 1,618), mais ce n’est pas une preuve de son utilisation délibérée : elle peut tout aussi bien être centrée, comme le suggère la figure 135, sur le format rationnel (de valeur décimale exacte 1,6) ou sur un autre format proche.
Toutes les « preuves » de l’utilisation du nombre d’or dans les proportions de la façade du Parthénon, avancées au xixe siècle et au début du xxe siècle dans le but d’étayer les interprétations de leurs auteurs, reposent sur des mesures ad hoc. Comme en statistiques, il est facile d’ajuster les données pour leur faire dire ce que l’on veut… Les mesures de la façade du Parthénon varient selon les auteurs en hauteur, selon le nombre de marches du soubassement prises en compte (ces marches sont bien trop hautes pour servir d’escalier), et en largeur, selon que la mesure est faite au ras des colonnes, aux bords de la toiture ou entre des verticales choisies à dessein. Sur les figures 140 et 141, les rectangles dans lesquels est inscrite la façade du Parthénon ne sont pas définis par rapport aux mêmes repères et ils ne se superposent pas.
Sur la figure 140, à quoi correspondent les carrés et les rectangles qui ont été superposés à la partie droite du fronton ? La figure 6 donne un pavage différent… Que dire de l’épaisseur des traits rouges, comparée à celle des traits de la figure 135, tracée à la même échelle ? Des études moins orientées ont montré que, dans la construction du Parthénon, plusieurs formats ont manifestement été utilisés. Par exemple, le quotient « largeur/hauteur » de la colonnade et le quotient « distance entre les colonnes/largeur des colonnes » sont tous deux proches de 9/4.
Depuis 150 ans, plusieurs études statistiques ont été faites afin de déterminer le format de rectangle jugé le plus esthétique. Les réponses varient selon la taille relative des rectangles, leur orientation et la manière dont ils sont disposés les uns par rapport aux autres. Dans l’expérience de Fechner (1875), trois quarts des réponses donnent comme plus harmonieux les rectangles de format compris entre 1,5 et 1,75, sans donner de préférence au rectangle d’or. Certains chercheurs ont conjecturé que cette préférence était liée à la zone centrale de vision de l’œil humain, qui est approximativement une ellipse inscrite dans un rectangle de format voisin de 1,5. Reste à prouver que c’est la bonne explication ! D’autres pensent que ce format se retrouve approximativement dans plusieurs proportions du corps humain, que nous trouvons évidemment plus harmonieux que d’autres.
Des expériences plus récentes ont confirmé ces résultats. En photographie argentique, les pellicules étaient le plus souvent de dimensions 24 mm × 36 mm, donc au format 3/2, de valeur décimale 1,5. En photographie numérique, il est souvent possible de choisir entre les formats 1/1, 3/2, 4/3 et 16/9. Nos écrans sont le plus souvent au format 4/3 ou 16/9, parfois 16/10 pour les smartphones. Il ne semble pas y avoir d’écrans au format 8/5 et il ne peut pas y en avoir au format exact du rectangle d’or : étant irrationnel, une au moins des dimensions de l’écran ne correspondrait pas à un nombre entier de pixels.
17. Le nombre d’or au Moyen Âge
17.1. L’âge d’or des cathédrales
L’âge d’or des cathédrales se situe entre le début du xie siècle (cathédrale de Strasbourg, 1015) et la fin du xiiie siècle (cathédrale d’Albi, 1282). L’architecture romane (voûtes d’arcs en plein cintre) a été utilisée entre le xe et le milieu du xiie siècle, l’architecture gothique (voûtes sur croisées d’ogive) ensuite, et jusqu’au xvie siècle.
Le nombre d’or et le rectangle d’or étaient a priori inconnus des bâtisseurs occidentaux jusqu’à la parution de De Divina Proportione. Cet ouvrage de Luca Pacioli, illustré par Léonard de Vinci, n’a été édité qu’en 1509, au début du xvie siècle, soit environ deux cents ans après la construction de la dernière de la cinquantaine de cathédrales érigées en France entre le xe et le xive siècle. Si les architectes médiévaux (alors appelés maîtres d’œuvre) n’utilisaient pas sciemment le nombre d’or dans leurs constructions, comment se fait-il que l’on retrouve des proportions qui semblent liées à ce nombre dans leurs constructions ? Nous allons voir que, pour cela, ils n’avaient pas à connaître le nombre d’or, ni à savoir construire géométriquement la division d’un segment en extrême et moyenne raison, ni celle d’un rectangle au format du nombre d’or : ils utilisaient simplement un système de mesures, le quine, matérialisé par la « canne des maîtres d’œuvre ».
Rappelons que le nombre d’or est irrationnel et que le rectangle d’or n’est pas constructible de manière simple avec une corde à treize nœuds. Si on suppose (ce qui est peu probable) que le nombre d’or était connu et utilisé par les bâtisseurs des cathédrales, la figure 142 donne l’une des constructions possibles d’un rectangle d’or. La figure 143 montre qu’il est nettement plus facile de construire un rectangle au format rationnel 8/5.
Pour construire la figure 142 :
- ABC est le triangle rectangle obtenu avec la corde à treize nœuds,
- AMD est un triangle rectangle d’hypoténuse
 ,
, - le cercle de centre D et de rayon DA = 1 coupe (MD) en E,
- puisque
 et DE = 1,
et DE = 1, 
- le cercle de centre M et de rayon ME coupe (AC) en N. Le rectangle MNPQ est un rectangle d’or puisque MN = 2φ et NP = 2 .
17.2. Le quine et la pige, ou canne des maîtres d’œuvre
Pour mesurer et reporter des longueurs, les bâtisseurs médiévaux utilisaient une canne graduée, la pige, ou une canne articulée construite sur le même principe. Cette canne portait une suite de cinq mesures, appelée « quine », dans laquelle :
- chaque mesure fait référence à une dimension du corps humain : paume (largeur de la paume de la main, environ 8 cm), palme (distance entre les extrémités de l’index et celle de l’auriculaire, doigts écartés, environ 12 cm), empan (distance entre les extrémités du pouce et de l’auriculaire, environ 20 cm), pied (environ 32 cm), coudée (distance entre l’extrémité de l’index et l’articulation du coude, environ 52 cm) ;
Ces dimensions approximatives ont été relevées sur le document de l’APMEP cité en bibliographie, auquel il semble raisonnable de faire confiance. Les largeurs de la paume, du palme, de l’empan, du pied et de la coudée sont évidemment variables d’une personne à une autre, mais les rapports entre deux de ces unités de mesure restent approximativement constants d’une personne à une autre. Chaque maître d’œuvre avait sa propre canne, dont les dimensions étaient plus ou moins normalisées, mais qui pouvaient changer au cours du temps et/ou d’une région à une autre.
- les parties du corps humain servant d’étalon ont des valeurs croissantes, choisies pour que chaque terme du quine soit approximativement la somme des deux termes précédents. Avec les valeurs ci-dessus, la moyenne du coefficient multiplicateur qui permet de passer d’un terme au suivant est égale à 1,6 ± 0,002. Rien de surprenant : on retrouve dans le quine l’algorithme de calcul des termes de la suite de Fibonacci. En effet, Fibonacci est bien le premier à avoir publié la définition de la suite qui porte son nom et qui est célèbre pour la manière dont il l’a illustrée, mais il n’en est pas l’auteur. La canne des maîtres d’œuvre était graduée selon cet algorithme bien avant 1202, date de la parution de Liber Abaci.
Le système de mesures au Moyen Âge était bien plus complexe. Selon l’article Ligne sur Wikipédia, l’unité de base était la ligne, qui mesurait 1/9 de paume, soit 4 grains d’orge. Au moment de la définition du mètre (10 décembre 1799), la ligne mesurait environ 2,256 mm. Par ordre croissant, on utilisait les unités suivantes, qui n’étaient pas toutes utilisées dans le quine :
- le doigt, qui mesurait 1/4 de paume, soit 9 lignes,
- le pouce, qui mesurait 1/3 de paume, soit 12 lignes,
- la paume, qui mesurait 34 lignes,
- le pied, qui mesurait 4 paumes, soit 144 lignes,
- la coudée, qui mesurait 6 paumes, soit 216 lignes,
- la toise, qui mesurait 24 paumes, soit 864 lignes.
Le quine normalisé (figure 144) comportait les cinq unités suivantes, qui sont des termes de la suite de Fibonacci :
- une paume de 34 lignes,
- un palme de 55 lignes (palme/paume = 1,5),
- un empan de 89 lignes (empan/palme ≈ 1,667),
- un pied de 144 lignes (pied/empan = 1,6),
- une coudée de 233 lignes (coudée/pied = 1,625).
Nous avons vu, page 17, que Kepler a prouvé, en 1608, que la limite du quotient ![]() de deux termes consécutifs de toute suite définie par l’algorithme de Fibonacci est égale au nombre d’or, de valeur approchée 1,618. De ce fait, même avec des quines différents du quine normalisé ci-dessus, on retrouve approximativement le nombre d’or dans les proportions, mesurées a posteriori, des bâtiments construits en utilisant cet outil.
de deux termes consécutifs de toute suite définie par l’algorithme de Fibonacci est égale au nombre d’or, de valeur approchée 1,618. De ce fait, même avec des quines différents du quine normalisé ci-dessus, on retrouve approximativement le nombre d’or dans les proportions, mesurées a posteriori, des bâtiments construits en utilisant cet outil.
En résumé :
- Fibonacci a publié Liber Abaci en 1202 ; à cette date l’algorithme qui définit la « suite de Fibonacci », ainsi que la suite elle-même, étaient tous deux connus probablement depuis longtemps ;
- Luca Paccioli a publié De Divina Proportione en 1509, date à laquelle la plupart des grandes cathédrales avaient été construites, alors que la division d’un segment en extrême et moyenne raison, donc le nombre d’or, était tombée dans l’oubli depuis l’Antiquité. Cet ouvrage est le point de départ de la renaissance du nombre d’or ;
- le lien entre le nombre d’or et la suite de Fibonacci n’a été établi, par Kepler, qu’en 1608. À cette date, l’âge d’or des cathédrales était terminé depuis deux siècles.
Aucune preuve historique ne permet de penser que le nombre d’or était connu des maîtres d‘œuvre avant la publication de De Divina Proportione, en 1509. Il est bien plus raisonnable de penser que le nombre d’or n’apparaît dans les proportions des cathédrales que parce que les maîtres d’œuvre ont utilisé le quine, gradué selon l’algorithme de Fibonacci, lequel était connu bien avant sa publication en 1202.
17.3. Le carnet de Villard de Honnecourt
Villard de Honnecourt est né dans le village de Honnecourt (département du Nord, à mi-chemin entre Cambrai et Saint-Quentin) aux environs de l’an 1200. Maître d’œuvre du xiiie siècle, il a laissé à la postérité l’un des rares documents de cette époque traitant d’architecture : un carnet conservé à la Bibliothèque nationale, qui contient des dessins de personnages, d’animaux, de diverses machines, de rosaces, d’éléments d’architecture, et quelques croquis à main levée (une version numérisée, au format pdf, est disponible sur le site de la BNF). Villard de Honnecourt a laissé d’autres documents ne figurant pas dans son carnet, dont un Canon de division harmonieuse qui donne une méthode pour déterminer les marges autour de la zone de texte des pages d’un livre, indépendante du format du livre ouvert. Cette méthode (figure 145) est encore enseignée de nos jours.
Pour construire la figure 145 :
- construire un rectangle ABDE, ici de format 4/3 et réunion des deux pages ABCF et CDEF de format 3/2 ;
- par le point H, mener la perpendiculaire à [EF], qui coupe ce segment en J ;
- le segment [JG] coupe le segment [DF] en L ;
- le texte de la page de gauche est délimité par le rectangle RQPK, celui de la page de droite par le rectangle LMNO.
Aucun des documents laissés par Villard de Honnecourt (qui a été au mieux de son art entre 1 225 et 1 250) ne contient la moindre référence au nombre d’or.
18. Le nombre d’or à la Renaissance : Luca Pacioli et Léonard de Vinci, la redécouverte du nombre d’or et la « divine proportion »
Le nombre d’or et le rectangle d’or n’ont probablement pas été utilisés à dessein, par les architectes et les artistes, avant la publication, en 1509, de De Divina Proportione, écrit par Luca Pacioli et illustré par Léonard de Vinci.
Luca Pacioli (né vers 1447, décédé en 1517) est un moine franciscain, connu pour diverses publications sur les mathématiques, dont une traduction en latin des Éléments d’Euclide. En 1494, il présente, dans son ouvrage Summa de arithmetica, geometria, de proportioni et de proportionalita, la comptabilité vénitienne, connue depuis sous le nom de « comptabilité en partie double ».
Dans son ouvrage, Corbalán (2010) donne une traduction des arguments que Luca Pacioli a avancés pour donner le nom de « divine proportion » à l’antique « section dorée », en s’appuyant sur des considérations religieuses qui ne reposaient plus sur la mythologie grecque, mais sur la foi chrétienne. Voici un résumé de ces arguments.
- De même que Dieu est unique, le nombre d’or est unique.
- De même que la Sainte Trinité regroupe le Père, le Fils et le Saint-Esprit, le nombre d’or est défini à partir de trois longueurs.
- De même que les voies du Seigneur sont impénétrables, le nombre d’or est irrationnel et nul humain ne peut en donner la mesure exacte.
- De même que Dieu est omniprésent dans l’univers, de la plus petite des créatures au cosmos entier, le nombre d’or est invariant par changement d’échelle : sa valeur ne dépend pas de la longueur du segment qui permet de le construire et se retrouve jusqu’à l’infiniment petit dans la construction autosimilaire d’un pentacle inscrit dans un pentacle (figure 146). L’Homme n’arrivera jamais à connaître le secret de la création.
- Le nombre d’or est indispensable à la construction du dodécaèdre (figure 147), qui représente le cinquième élément utilisé par Dieu pour créer le cosmos, les quatre premiers étant la terre, l’eau, l’air et le feu.
Dans De Divina Proportione, on retrouve explicitement, et pour la première fois depuis l’Antiquité, la division d’un segment en extrême et moyenne raison, diverses constructions du pentagone régulier et des solides pythagoriciens, et une utilisation du nombre d’or. Léonard de Vinci a-t-il lui-même systématiquement utilisé le nombre d’or et le rectangle d’or dans les dessins de cet ouvrage, hors constructions géométriques liées au pentagone ? Apparemment pas…
Dans la planche intitulée Divina Proportio, reproduite sur la figure 148 (les lettres en caractères rouges ont été rajoutées pour faciliter la lecture), L. de Vinci inscrit un visage humain dans un rectangle ABCD de format voisin de 1,16.
Il superpose à celui-ci :
- un triangle ABE qui semble équilatéral ;
- plusieurs rectangles verticaux : le format de ABLI est voisin de 1,73, celui de HKCD est voisin de 1,69 et les formats des autres sont encore plus éloignés de 1,618 ;
- deux rectangles horizontaux : le format de AFED est 1,71 et le format de FBCE est 1,67.
Dans son dessin de l’Homme de Vitruve (figure 149), qui ne figure pas dans De Divina Proportione, L. de Vinci inscrit un homme « bras étendus levés et jambes écartées » dans un cercle, dont le centre est au nombril du personnage et « bras étendus horizontaux et jambes serrées » dans un carré, dont le centre est aux organes sexuels du personnage.
Vitruve est un architecte romain qui a vécu au ier siècle av. J.-C. Dans De Architectura, il décrit des proportions idéalisées de l’homme, mais il n’utilise ni la division en extrême et moyenne raison ni a fortiori le nombre d’or et le rectangle d’or.
Le dessin original peut être interprété comme une représentation allégorique, qui – de manière très anthropocentrique, mais on n’est jamais si bien servi que par soi-même – place l’homme au centre de l’univers. Il ne comporte pas le pentagone ajouté par certains comme « preuve » des relations entre cette figure et le pentagone ou le nombre d’or. Le texte, difficilement lisible car il est écrit en miroir, fait référence au traité de Vitruve, mais pas au nombre d’or (voir Homme de Vitruve sur Wikipédia).
Léonard de Vinci a-t-il utilisé le nombre d’or dans le dessin de l’Homme de Vitruve ? Aux erreurs de mesure près (rappelons que des mesures sur un dessin ou un plan ne sont pas acceptées par les tribunaux), les rapports habituellement considérés comme preuves de cet usage sont proches du nombre d’or. En effet, autant que l’on puisse se fier à de telles mesures, on trouve AC / BC ≈ 1,64, BC/AB ≈ 1,57 et côté du carré / rayon du cercle ≈ 1,65. Noter que la longueur des bras est identique lorsqu’on passe d’une position à l’autre.
Si Léonard de Vinci avait voulu faire apparaître le nombre d’or dans ce dessin, il l’aurait probablement fait de manière plus précise et il l’aurait peut-être dit, ce qu’il n’a pas fait. En réalité, de Vinci ne fait pas entrer l’Homme de Vitruve dans un rectangle d’or ou dans un pentagone (que certains n’hésitent pas à superposer au dessin), mais dans une figure légèrement modifiée d’un « carré de Mercure ».
Il est probable que la modification des dimensions habituelles du carré de Mercure a été faite pour que la longueur des bras soit la même dans le cercle et dans le carré, l’animation suggérée du corps paraissant ainsi plus réaliste.
Un carré de mercure (figure 150) donne une approximation de la construction d’un carré de même périmètre que celui d’un cercle. Dans cette construction, la valeur exacte du quotient côté du carré/rayon du cercle est égale à 8/5, dont la valeur décimale ne diffère de celle du nombre d’or que d’environ 2 %. Est-il surprenant que l’on puisse penser que Léonard de Vinci a utilisé le nombre d’or lorsqu’il a dessiné l’Homme de Vitruve ?
Pour construire la figure 150 :
- tracer le triangle OAB, rectangle en A, avec la corde à treize nœuds,
- tracer le cercle (c), de centre O et de rayon 5, passant par B,
- terminer la construction du carré BCDE, de côté 8.
Avec l’unité de la corde à nœuds, le périmètre du carré BCDE mesure 32 unités et le périmètre du cercle (c) mesure 2 x π x 5 unités, de valeur approchée 31,416 unités. Comme 32 /10 x π ≈ 1,0186, le pourcentage d’écart entre le périmètre du carré et celui du cercle est d’environ 2 %.
Cette construction est à mettre en parallèle avec le célèbre problème de la quadrature du cercle, qui consiste à construire, à la règle et au compas, un carré de même aire qu’un disque donné. Sujet de recherches infructueuses depuis l’Antiquité, l’impossibilité de la quadrature du cercle n’a été démontrée qu’en 1768, lorsque Jean-Henri Lambert a donné la preuve de l’irrationalité de . On trouve encore, sur Internet, des constructions géométriques qui prétendent réussir cette quadrature. En réalité, elles n’en donnent qu’une bonne approximation (glossaire, figure 156, qui utilise la corde à treize nœuds, est l’une des meilleures). On trouve aussi, sur Internet, des « preuves » que la Terre est plate…
Finalement, dans De Divina Proportione, le nombre d’or et le rectangle d’or n’apparaissent explicitement que dans les textes et les figures qui décrivent la division d’un segment en extrême et moyenne raison, dans la construction du pentagone régulier et dans leurs applications mathématiques, comme la construction du dodécaèdre régulier. Léonard de Vinci ne dit pas avoir explicitement utilisé le nombre d’or dans son célèbre dessin de l’Homme de Vitruve.
19. Le nombre d’or de la Renaissance au xviie siècle et le renouveau des secrets ésotériques
19.1. Dürer et Kepler
Dürer (1471-1528), artiste et mathématicien, publie en 1525 Instructions pour la mesure à la règle et au compas, l’un des premiers livres de mathématiques rédigés en allemand. Il y donne des constructions des polygones réguliers et il utilise des patrons pour construire des polyèdres par pliage et collage. Il reprend l’idée de Pacioli et de Léonard de Vinci, selon laquelle la beauté a des bases géométriques.
Grâce à ses propres observations astronomiques et de longs calculs, l’astronome Kepler (1571-1630) détermine, avec une précision inégalée pour l’époque, les orbites des planètes. On lui doit les « trois lois de Kepler », dans lesquelles il établit que ces orbites sont des ellipses, et non des cercles parfaits, et décrit la manière dont ces orbites sont décrites.
Convaincu que les mathématiques – en particulier le nombre d’or, le pentagone et leurs multiples propriétés – sont le fondement de l’harmonie de la création divine, Kepler échafaude un modèle cosmologique dans lequel il essaie de mettre en concordance ses observations scientifiques avec ses convictions religieuses, fortement mêlées de croyances astrologiques et d’interprétations ésotériques. Sur la base de correspondances approximatives entre les orbites qu’il avait lui-même calculées pour les planètes et les propriétés des solides platoniciens, Kepler associe chaque planète à l’un de ces solides : il range ces derniers (par nombre croissant de faces) dans des sphères concentriques de diamètres croissants, chaque solide contenant une sphère inscrite, tout en étant lui-même inscrit dans la sphère de diamètre immédiatement supérieur. Cette théorie farfelue était loin de faire l’unanimité de ses confrères astronomes, mais il n’en reste pas moins que Kepler est l’un des fondateurs de l’astronomie et de la science modernes. C’est en 1608 qu’il prouve que, si un et un+1 sont deux termes consécutifs de la suite de Fibonacci, leur quotient ![]() a pour limite le nombre d’or lorsque n tend vers l’infini.
a pour limite le nombre d’or lorsque n tend vers l’infini.
19.2. Le nombre d’or du xviie siècle à nos jours
Jusqu’à preuve du contraire, l’affirmation selon laquelle le nombre d’or a été systématiquement et en secret utilisé par les architectes et les artistes, pendant toute l’antiquité et le Moyen Âge, relève d’un mythe moderne.
Rappelons-le : la figure 135 montre à l’évidence que de simples proportions, mesurées a posteriori et de manière ad hoc, ne peuvent pas être considérées comme des preuves de l’utilisation du nombre d’or et du rectangle d’or. Les preuves ne peuvent être validées que par des faits ou des documents historiques indiscutables, de préférence vérifiables par recoupements de sources fiables, indépendantes et concordantes.
Ce mythe aurait pris sa source au xvie siècle ou au xviie siècle, probablement à la suite de la publication de De Divina Proportione et des travaux de Kepler, dont la renommée était grande dans l’Europe entière. Il a été fortement amplifié entre la fin du xixe siècle et le début du xxe siècle où, à la suite de nouvelles interprétations historiquement infondées, il s’est de nouveau trouvé entouré de mystères, dans un monde d’initiés, comme il l’était à l’origine dans l’école pythagoricienne.
À partir de cette époque, plusieurs écoles de peinture (les nabis, les expressionnistes, les fauvistes, les cubistes, etc.) ont utilisé le nombre d’or, mais – semble-t-il – pas aussi systématiquement que veulent le faire croire certains. Le principal promoteur du nombre d’or fut Le Corbusier (Charles-Edouard Jeanneret-Gris, né en 1887 et décédé en 1965), qui l’a utilisé pour définir le Modulor, norme architecturale et artistique empreinte de mysticisme, dans lequel il définit des « proportions naturelles », présentées comme idéales, à partir des dimensions du corps humain, du nombre d’or et de la suite de Fibonacci. Ceci n’enlève rien à son talent d’architecte… mais sa vision fortement anthropocentrique est typique de la civilisation occidentale, qui ramène tout à l’Homme depuis l’Antiquité. D’autres civilisations ont vu (ou voient) le monde autrement…
Les humains ont toujours aimé les régularités, qu’elles soient ou non liées au nombre d’or. Ils ont aussi toujours aimé les mythes, et celui qui entoure le nombre d’or est extraordinairement répandu : sur Google®, consulté début 2020, la requête Nombre d’or et beauté renvoie, en quelques secondes, à plus de 55 000 000 références et la requête Nombre d’or et architecture renvoie à plus de 340 000 000 références !
Conclusion
Les étonnantes propriétés mathématiques conjointes du nombre d’or, de l’angle d’or, des spirales et de la suite de Fibonacci ne peuvent que susciter et stimuler la curiosité et l’imagination. Chez les végétaux, la présence du nombre d’or est avérée. Associée à une spirale générative, la suite de Fibonacci apparaît parce que l’angle de divergence entre deux organes en croissance est le plus souvent l’angle d’or, ou un autre angle lié aux premiers termes de la suite de Fibonacci.
Le nombre d’or n’a probablement pas été utilisé sciemment dans les proportions des monuments antiques. Pour la pyramide de Khéops, son hypothétique présence résulte de mesures effectuées plus de deux mille ans après la construction du monument et repose sur des considérations mathématiques et des méthodes de calcul qui ne pouvaient pas être connues il y a 4 500 ans. Pour le Parthénon, son architecte pouvait connaître le nombre d’or, mais l’utilisation supposée de ce nombre ne repose que sur des mesures ad hoc, datant du xixe ou du xixe siècle, qui plus est différentes selon les auteurs. Dans les deux cas, il n’existe aucune preuve historique de ces interprétations.
Lors de la construction des cathédrales, les proportions attribuables au nombre d’or peuvent être justifiées par le système de mesures des maîtres d’œuvre, fondé sur la suite de Fibonacci, ce qui ne demandait pas de connaître explicitement le nombre d’or.
Que les inconditionnels des interprétations magiques et ésotériques du nombre d’or (et de son utilisation universelle en architecture et dans les arts depuis la plus haute Antiquité) me pardonnent d’en avoir seulement une vision scientifique… Cette vision est bien moins mystérieuse, mais n’est-elle pas tout aussi riche et étonnante ?
De l’avis des mathématicien-ne-s, les nombres n’ont pas besoin d’interprétations ésotériques pour devenir magiques… Pensez au nombre ![]() .
.
Crédit illustrations
À l’exception de quelques illustrations (figures 140, 141, 147, 148, 149), les photographies, les figures géométriques, les schémas et les tableaux sont de l’auteur.
Pour refaire les figures
Toutes les figures géométriques ont été construites à l’aide du logiciel libre Geogebra, en téléchargement gratuit sur www.geogebra.org. Les notions mathématiques utilisées dans cet article sont, pour l’essentiel, compréhensibles par des lycéens de classe de terminale qui étudient les mathématiques.
Glossaire et compléments
Algorithme (n. m.)
Suite finie de calculs et/ou d’instructions permettant de trouver une solution à un problème. De nombreux algorithmes reposent sur des calculs itératifs, effectués en boucle à partir des résultats des calculs précédents. Les opérations correspondantes peuvent être effectuées à la main ou à l’aide d’un ordinateur.
Algorithme de Fibonacci (n. m.)
Algorithme définissant une suite numérique dans laquelle, une fois les deux premiers termes donnés, chaque terme suivant est la somme des deux termes qui le précèdent : un+2 = un+1 + un. Les deux premiers termes de la suite de Fibonacci sont classiquement u0 = 1 et u1 = 1. On peut aussi partir de u0 = 0 et u1 = 1, choix qui conduit à la même suite de nombres, avec un simple décalage d’indices.
Angiosperme (n. f.)
Nom scientifique des plantes à fleurs. Les Angiospermes ont des ovules enfermés dans un ovaire, contrairement aux Gymnospermes, dont les ovules sont nus.
Alternes (feuilles)
Feuilles isolées les unes des autres (une seule feuille par nœud), habituellement disposées en hélice le long de la tige.
Angle d’or
Angle au centre qui intercepte, dans un cercle, le plus petit des deux arcs qui partagent la circonférence en extrême et moyenne raison (figure 2).
Apex (n. m.)
Extrémité d’une pointe.
Apical
Situé à l’apex.
Association végétale
L’association végétale est l’unité de base de la classification phytosociologique, qui étudie les communautés végétales en mettant en évidence les liens entre les espèces qui les composent et entre ces espèces et leur milieu de vie.
Axillaire
Se dit d’un organe ne naissant pas au sommet de la tige, mais sur la tige elle-même (ou sur l’un de ses rameaux), à l’aisselle d’une bractée ou du pétiole d’une feuille.
Bractée (n. f.)
Feuille modifiée que l’on observe sur le pédicelle d’une fleur ou d’une inflorescence, à la base des rameaux d’une inflorescence ramifiée ou encore à la base d’une inflorescence condensée (par exemple dans l’involucre d’un capitule).
Bractéole (n. f.)
Petite bractée à la base du pédicelle d’une fleur dans une inflorescence composée.
Calice (n. m.)
Partie inférieure du périanthe, formée d’un verticille de sépales. Le calice protège le reste de la fleur lors de son développement et jusqu’à son épanouissement.
Capitule (n. m.)
Inflorescence condensée, regroupant des fleurons (petites fleurs sans pédicelle) serrés les unes contre les autres sur un réceptacle en forme de disque, de calotte sphérique, etc.
Carpelle (n. m.)
Pièce florale femelle, formée d’un ovaire abritant l’ovule (ou les ovules). L’ovaire est surmonté du style et du stigmate, qui reçoit le pollen. Voir l’illustration à l’entrée Fleur.
Caulinaire
Relatif à la tige.
Cône (n. m.)
En botanique : un cône est un rameau dont l’axe raccourci porte, abrités par des écailles, les organes reproducteurs chez une partie des Gymnospermes (Cupressacées et Pinacées, habituellement appelées conifères : cyprès, pins, sapins, épicéas, mélèzes, genévriers, etc.) :
- les cônes mâles portent les étamines ; ils sont caducs après libération du pollen ;
- les cônes femelles portent des ovules nus. Après fécondation et sauf exceptions (genévriers, ifs), leurs écailles se lignifient. Chez les cèdres et les sapins, les cônes libèrent les graines en se désarticulant sur l’arbre en fin de saison. Chez les pins, les cônes restent entiers et ne sont mûrs qu’au bout de deux ans : par temps sec, leurs écailles s’écartent et libèrent les graines.
Conifère (n. m. et adj.)
Littéralement « porte cône ». Arbre de la classe des Gymnospermes, dont les ovules nus sont abrités par les écailles d’un cône : pins, sapins, genévriers, épicéas, cèdres, mélèzes, etc.
Conjecture (n. f.)
Supposition vraisemblable, mais restant à démontrer.
Convexe
En mathématiques, se dit d’un domaine fermé, contenant en entier tout segment reliant deux de ses points.
Corde à treize nœuds
Corde portant treize nœuds régulièrement espacés, délimitant (lorsqu’elle est tendue) douze segments de même longueur. La corde à treize nœuds permet de tracer un triangle rectangle de côtés respectifs 3, 4, 5 (figure 134) et d’autres figures géométriques simples, comme un triangle équilatéral de côté 4. Utilisée comme un simple cordeau, elle permet de reporter des distances, de tracer de cercles, etc. On peut évidemment fabriquer une corde d’arpenteur à plus de treize nœuds…
Corolle (n. f.)
Partie supérieure du périanthe, formée d’un verticille de pétales. La corolle, qui entoure les étamines et le pistil, est un signal visuel et une piste d’atterrissage pour les pollinisateurs.
Corrélation (n. f.)
Lien apparent entre des évènements, pouvant traduire une relation de cause à effet (évènements dépendants), mais pouvant aussi être observé par hasard et ne pas traduire une telle relation (évènements indépendants). Pour ne pas conclure trop hâtivement que des évènements sont dépendants, voir J.-L. Delahaye, 2017. Coïncidences surprenantes, mais banales, Pour la Science, n° spécial 481 : 108-113 (sur Internet, entrer la requête Jean-Luc Delahaye coïncidences surprenantes, mais banales puis, sur la page de résultats, aller sur le site cristal.univ-lille).
Corymbe (n. m.)
Inflorescence ressemblant à une grappe, dans laquelle les pédicelles inférieurs s’allongent, amenant toutes les fleurs à un même niveau (figure 153).
Degré (n. m.)
En mathématiques, mesure d’un angle dont le sommet est le centre d’un cercle et qui intercepte sur celui-ci un arc de longueur 1/360° de son périmètre. Le cercle complet correspond à un angle au centre de 360°, un demi-cercle à un angle de 180°, un quart de cercle à un angle de 90°, etc.
Décussées
Dans la phyllotaxie opposée-décussée, qualifie deux paires successives de feuilles décalées, vues dans l’axe de la tige, d’un quart de tour.
Dicotylédone (n. f.)
Plante dont l’embryon comporte deux cotylédons (préfeuilles contenant une réserve nutritive permettant le développement initial de la plantule). Exemple : le haricot.
Distique
Disposé sur deux rangs opposés. Dans une phyllotaxie distique, les feuilles sont situées de part et d’autre de la tige et leur angle de divergence mesure 180°.
Divergence (angle de)
Angle formé par les pétioles de deux feuilles consécutives, mesuré perpendiculairement à l’axe de la tige.
Division d’un segment « en extrême et moyenne raison »
Le langage des mathématiciens de l’Antiquité était très différent de celui que nous utilisons actuellement :
- le mot raison est à prendre au sens de son étymologie latine ratio, qui désigne de manière générale un calcul – ou une méthode de calcul – et en particulier le rapport de deux grandeurs, exprimé sous forme de quotient (ou de pourcentage, comme actuellement en économie ou en finance, mais les pourcentages n’étaient pas utilisés dans l’Antiquité) ;
- dans l’expression « division d’un segment en extrême et moyenne raison » les valeurs « extrêmes », a +b et b sont toutes deux comparées à la valeur « moyenne » (au sens de valeur intermédiaire).
Sur la figure 1, pour justifier que l’on a bien AB/AC = AC/BC :
- avec OB pour unité, AB = 2 ; d’après le théorème de Pythagore,
 ;
; - vérifier que
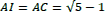 et que
et que  ;
; - conclure en comparant les valeurs de AB/AC et de AC/BC.
Dodécaèdre régulier
Polyèdre dont chacune des douze faces est un pentagone régulier.
Équation polaire
Relation liant les coordonnées polaires d’un point appartenant à une droite ou à une courbe donnée. Exemple : en coordonnées cartésiennes, l’équation d’un cercle de centre O et de rayon 1 est x² + y² = 1. En coordonnées polaires, ce même cercle a pour équation r(t) = 1, t prenant ses valeurs dans l’intervalle [0 ; 2π].
Étamine (n. f.)
Pièce florale contenant le pollen.
Exponentielle (n. f.)
En mathématiques, l’exponentielle est une fonction numérique, notée exp, égale à sa propre fonction dérivée, telle que l’image de 0 est égale à 1. On montre que exp(1) = exp, égalité dans laquelle e est un nombre irrationnel de valeur décimale approchée 2,718. La fonction exponentielle transforme une somme en produit et une différence en quotient :
exp (x + x’) = exp (x) x exp (x’) et exp (x – x’) = exp (x) / exp (x’)
et
Comme cette propriété se retrouve dans les calculs sur les puissances (par exemple dans l’égalité 10a+b = 10ax 10b), la relation y = exp (x) est habituellement notée y = ex. La fonction exponentielle sert à modéliser des phénomènes dans lesquels un accroissement constant (égal à k) de la variable se traduit par un rapport constant (égal à ek) entre les images correspondantes :
si x’ + x = k, alors ex’-x = ex’/ex = ek (voir spirale exponentielle).
À ce titre, la fonction exponentielle intervient dans les équations différentielles, relations entre une fonction numérique et sa dérivée ou ses dérivées successives.
Feuille (n. f.)
Organe d’une plante qui, présentant à la lumière une surface importante, assure habituellement la photosynthèse.
Fibonacci, suite de… ou algorithme de…
Suite numérique additive, définie par ses deux premiers termes u0 et u1 et la relation linéaire récurrente un+2 = un+1+ un. Les onze premiers termes de cette suite, telle que définie par Fibonacci, sont 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… Prendre 0 et 1 comme premiers termes ne fait que décaler d’une unité le rang des termes suivants.
Fleur (n. f.)
La fleur est l’organe assurant la reproduction sexuée chez les Angiospermes.
- Chez une espèce hermaphrodite, la fleur est habituellement composée d’un périanthe de sépales et de pétales, qui abrite simultanément la partie mâle (étamines) et la partie femelle (pistil).
- Chez une espèce monoïque, un même pied porte deux sortes de fleurs : les unes mâles (seules les étamines sont fonctionnelles) et les autres femelles (seuls les pistils sont fonctionnels).
- Chez une espèce dioïque, les fleurs mâles et les fleurs femelles sont portées par des pieds distincts.
Fleuron (n. m.)
Fleur élémentaire, sans pédicelle, portée par un capitule.
Format d’un rectangle (n. m.)
Rapport L/l de la longueur L à la largeur l (page 6).
Fractale
Une structure est fractale lorsque ses motifs se répètent, à l’identique et récursivement, à l’intérieur d’eux-mêmes. Une telle structure, invariante par changement d’échelle, est bien illustrée par le chêne de la figure 70 et par le chou romanesco de la figure 120. Avez-vous remarqué que cette invariance par changement d’échelle se retrouve aussi bien sur le développement en fraction continue du nombre d’or (pages 5 et 16), qui peut être considéré comme un nombre fractal, que sur les spirales exponentielles, qui sont des figures fractales « lisses ».
Fraction continue
Une fraction continue permet de représenter tout nombre réel x sous la forme
Voir, page 5, comment trouver la fraction continue qui donne des valeurs approchées successives, de plus en plus précises, du nombre .
Fractions égyptiennes
En mathématiques, le développement d’une fraction en fractions égyptiennes consiste à l’écrire comme somme de fractions de numérateur 1 et de dénominateur entier naturel. Cette décomposition n’est pas unique.
Par exemple : 2/5 = 1/5 + 1/5 = 1/5 + 1/6 + 1/30 = 1/5 + 1/8 + 1/8 + 1/40, etc.
Pour développer une fraction en fractions égyptiennes, plusieurs algorithmes sont connus. Voici celui attribué à Fibonacci : partant de la fraction a/b avec a < b,
- déterminer le plus petit entier n tel que n > 1 /(a/b), c’est-à-dire tel que n > b/a ;
- la relation a/b = 1/n + (a/b – 1/n) conduit à a/b = 1/n + (a x n- b)/ b x n ;
- recommencer le processus avec la fraction (a x n- b)/ b x n
Il est prouvé que cet algorithme conduit toujours à un résultat en un nombre fini d’itérations, mais il peut conduire à une décomposition en fractions de dénominateurs très élevés.
Appliquons l’algorithme de Fibonacci à la fraction 2/5 :
- le nombre entier immédiatement supérieur à 5/2 est 3 ;
- 2/5 = 1/3 + (2/5 – 1/3) = 1/3 + 1/15
On peut continuer en décomposant 1/3 :
- le nombre entier immédiatement supérieur à 3 est 4 ;
- 1/3 = 1/4 + (1/3 – 1/4) = 1/4 + 1/12
Alors 2/5 = 1/4 + 1/12 + 1/15
On pourrait continuer le processus en décomposant 1/15 puis chacune des fractions ainsi obtenues. Le résultat obtenu est différent de celui qui a été trouvé au premier exemple.
Gymnosperme (n. f.)
Plante à graines, mais pas à fruits, dont les ovules nus ne sont pas contenus dans un ovaire.
Hélice (n. f.)
En mathématiques, courbe géométrique obtenue par l’enroulement d’un fil autour d’un solide de révolution (cylindre, cône, ogive, etc.). Si l’hélice est portée par un cylindre, sa projection sur un plan perpendiculaire à l’axe du cylindre est un cercle ; dans ce cas, le « pas » de l’hélice est la distance entre deux spires jointives, mesurée parallèlement à l’axe du cylindre. Si l’hélice est portée par un cône ou une ogive, sa projection sur un plan perpendiculaire à l’axe du cône ou de l’ogive est une spirale.
Hexagone régulier (n. m.)
Polygone régulier convexe à six côtés.
Hexagramme
Hexagone étoilé – ou « étoile à six branches » ou « étoile de David », etc. – que l’on peut inscrire dans un hexagone régulier convexe de mêmes sommets. Il est facile de tracer un hexagramme avec une corde à treize nœuds.
Hexastique
Disposé sur six rangs.
Icosaèdre régulier (n. m.)
Polyèdre dont chacune des vingt faces est un triangle équilatéral.
Incommensurable (nombre)
En mathématiques, qualification ancienne d’un nombre actuellement appelé irrationnel.
Indice (n. m.)
En mathématiques, nombre précisant le rang (ordre de calcul) du terme d’une suite. Lorsque le premier terme est u1, le terme un est le terme de rang n. Lorsque le premier terme est u0, le terme un est le terme de rang n+1.
Indice de phyllotaxie
Chez une plante dont la phyllotaxie est alterne-spiralée, l’indice de phyllotaxie est le rapport A/B entre le nombre A de spires et le nombre B d’entrenœuds qui séparent deux feuilles occupant approximativement la même position sur la tige. Les nombres et sont habituellement deux termes de la suite de Fibonacci, d’indices respectifs n et n +2.
Inflorescence (n. f.)
Disposition des fleurs sur la tige d’une plante à fleur. Par extension, partie de la plante portant les fleurs. Une inflorescence peut être simple (la figure 153 schématise les inflorescences simples les plus courantes) ou composée (un exemple est donné sur la figure 154). Pour une description plus complète, se reporter au Dictionnaire illustré de botanique (Jouy & de Foucault, 2016), pages 412 à 414.
Légende des inflorescences simples schématisées sur la figure 153 :
- Dans les inflorescences indéfinies, les fleurs se développent puis s’épanouissent « de la base vers le sommet » de l’axe principal, qui poursuit simultanément sa croissance. Exemples :
- 1a : épi simple, chez une partie des Poacées ;
- 1b : chaton, chez Corylus avellana, les aulnes, les bouleaux, les peupliers, le noyer, etc. ;
- 1c : grappe, chez le Phytolacca americana (figure 23), les scilles, les orchidées, les muscaris (figure 30), et de très nombreuses autres espèces ;
- 1d : corymbe, chez Ornithogalum umbellatum (figure 51) ;
- 1e: ombelle simple, chez une partie des Apiacées (anciennes Ombellifères), mais aussi chez Allium ursinum et Hedera helix ;
- 1f : capitule, chez les Asteracées (figures 103 à 119) ;
- 1g : glomérule, chez de nombreuses Juncacées et Cyperacées ;
- 1h : spadice, chez Arum italicum.
- Dans les inflorescences définies, les fleurs se forment « du sommet vers la base », ce qui demande une explication. La première fleur termine l’axe principal, dont la croissance s’arrête. Chaque suivante, de manière récursive, termine à son tour la ramification qui la porte et qui s’est développée au-dessous de la fleur précédemment formée. Ce processus conduit à une structure fractale dans laquelle, au final, le sommet de l’axe principal n’est pas visuellement perçu comme « sommet » de l’inflorescence… que l’on voit plutôt dans les dernières fleurs formées. Exemples (non illustrés) :
- 2a : cyme bipare, chez Datura stramonium;
- 2b : cyme unipare hélicoïde, chez Solanum dulcamara ;
- 2c : cyme unipare scorpioïde, chez Myosotis scorpioides.
Les inflorescences composées peuvent être formées :
- de plusieurs inflorescences simples d’un même type : épis d’épillets de Lolium perenne (figure 38), grappes de grappes ou panicules (nombreuses Poacées), ombelles d’ombellules de Daucus carota (figure 121), cymes de cymes (figure 154) et même capitule de capitules de Leontopodium nivale alpinum (figure 119), etc.
- de plusieurs types d’inflorescences simples de types différents : épi de cymes, épi de glomérules, grappe de cymes (ou thyrse), panicule d’épillets, corymbe de capitules (Achillea millefolium), etc.
Involucre (n. m.)
Ensemble des bractées qui entourent la base d’une inflorescence. La figure 103 montre l’involucre d’un capitule de Silybum marianum.
Irrationnel (nombre)
En mathématiques, nombre qui ne peut pas s’exprimer sous forme d’un quotient de deux nombres entiers.
Itérer/itération
Exécuter au moins deux fois de suite une même opération ou un même processus / action correspondante.
Limbe (n. m.)
Partie habituellement large, mince et aplatie d’une feuille, dans laquelle se produit la photosynthèse.
Logarithme (fonction)
Les fonctions logarithmes permettent de transformer une suite géométrique de nombres strictement positifs en une suite arithmétique.
La fonction « logarithme décimal », notée log, trouve son origine dans les règles de calcul sur les puissances de 10 : sachant que 10a x 10b = 10a+b et que 10a / 10b = 10a-b, si nous posons x = 10a et y = 10b, puis a = logx et b = logy , alors log (x x x’) = logx + logx’ et log (x/x’) = logx + logx’. On notera que, par leur définition, x et y sont tous deux strictement positifs : la fonction log n’est définie que sur l’intervalle ![]() .
.
Après avoir calculé une table de logarithme décimal, on peut l’utiliser pour réduire la complexité des calculs effectués en base dix : la fonction log permet de remplacer le produit de deux nombres x et y par la somme de leurs logarithmes et le quotient de ces deux nombres par la différence de leurs logarithmes. On obtient une valeur approchée du résultat en lisant la table en sens inverse. La règle à calcul, qui n’est plus guère utilisée, fonctionne sur ce principe : elle permet d’additionner ou de soustraire des longueurs de segments à l’aide d’une réglette mobile, sans donner (par exemple sur un chantier) de nombreuses décimales illusoires.
Encore faut-il pouvoir déterminer le logarithme de tout nombre strictement positif x , ce qui revient à calculer le nombre (non entier lorsque x n’est pas une puissance de 10) tel que x = 10a. Les premières tables de logarithmes ont été calculées à la main, par insertion de termes de suites géométriques : d’abord entre 1 et 10 (pour obtenir log 2 ; log 3 ; … ; log 9), ensuite et récursivement entre 1 et 2 (pour obtenir log 1,1 ; log 1,2 ; … ; log 1,9), etc., puis entre 1,1 et 1,2 (pour obtenir log 1,11 ; log 1,12 ; …. ; log 1,19), etc. Les calculs ont été répartis entre de nombreux scientifiques européens, avec vérification des résultats par les pairs. On comprendra qu’il ait fallu plusieurs dizaines d’années avant d’obtenir des tables suffisamment détaillées pour obtenir des calculs précis. Les tables de logarithmes ont été utilisées jusqu’à la mise sur le marché des premières calculatrices électroniques scientifiques de poche (aux environs de 1975).
La fonction « logarithme naturel » ou « logarithme népérien » (du nom du mathématicien écossais John Napier) est une fonction essentielle en mathématiques : c’est la primitive de la fonction inverse sur l’intervalle ![]() et la fonction réciproque de la fonction exponentielle. Comme toute fonction logarithme, elle transforme un produit en somme et un quotient en différence :
et la fonction réciproque de la fonction exponentielle. Comme toute fonction logarithme, elle transforme un produit en somme et un quotient en différence :
Méristème (n. m.)
Un méristème primaire est un petit groupe de cellules indifférenciées (cellules souches végétales), situé à l’extrémité de la tige d’une plante, mais aussi à l’extrémité de ses rameaux et de ses racines. Les cellules de l’apex du méristème se divisent tout en restant indifférenciées, alors que celles de sa périphérie se divisent en assurant simultanément la croissance en longueur de la tige et la formation des tissus spécialisés et des organes qu’elle porte. Chez les végétaux produisant du bois, un méristème secondaire, situé sous l’écorce, assure la croissance en diamètre du tronc et de ses ramifications.
Monocotylédone (n. f.)
Plante dont l’embryon comporte un seul cotylédon (préfeuille contenant une réserve nutritive permettant le développement initial de la plantule). Exemples : le blé, l’avoine.
Monostique
Disposé sur un seul rang.
Morphogenèse (n. f.)
Processus de formation et de développement d’un être vivant.
Moyenne arithmétique
En mathématiques, la moyenne arithmétique de deux nombres a et b est le nombre ma égal à (a + b) / 2.
Moyenne géométrique
En mathématiques, la moyenne géométrique de deux nombres positifs a et b est le nombre mg égal à ![]() , ce qui équivaut à dire que mg² = a x b. En d’autres termes, mg est le côté d’un carré de même aire que le rectangle de côtés a et b (quadrature du rectangle).
, ce qui équivaut à dire que mg² = a x b. En d’autres termes, mg est le côté d’un carré de même aire que le rectangle de côtés a et b (quadrature du rectangle).
Nœud (n. m.)
En botanique, point d’insertion d’une feuille sur la tige.
Nombre d’or (n. m.)
Dans la division d’un segment de longueur a + b, avec a > b en extrême et moyenne raison (page 3), le nombre d’or φ est la valeur commune des quotients a/b et (a + b) / a.
Octaèdre régulier (n. m.)
Polyèdre dont chacune des huit faces est un triangle équilatéral.
Octostique
Disposé sur huit rangs.
Opposées (feuilles)
Les feuilles opposées sont groupées par paires sur un même nœud et disposées de part et d’autre de la tige, avec un angle de divergence de 180°.
Organe (n. m.)
Partie d’un être vivant, qui a une fonction précise.
Orthostiche (n. f.)
Alignement radial des feuilles, lorsque l’angle de divergence entre deux feuilles est un diviseur de 360°.
Paramètre (n. m.)
En mathématiques, valeur numérique qui fixe les conditions initiales d’un calcul. Plus généralement, valeur numérique ou autre information qui intervient dans une théorie, un réglage (par exemple en informatique), etc.
Parastiches (n. f.)
Spirales secondaires qui apparaissent, dans les phyllotaxies alternes, lorsque les organes sont serrés : feuilles sur la tige, fleurs dans une grappe ou une ombelle, bractées et fleurons sur un capitule.
Pédicelle (n. m.)
Petit axe portant l’une des fleurs d’une inflorescence. En langage vernaculaire, le pédicelle est la « queue » d’une fleur.
Pédoncule (n. m.)
Partie terminale d’une tige, portant une inflorescence.
Penta (préfixe) / pentagone / pentagramme / pentacle (n. m.)
Penta est un préfixe grec indiquant une relation avec le nombre cinq.
- Un pentagone régulier est un polygone convexe à cinq côtés, tous de même longueur, inscriptible dans un cercle.
- Un pentagramme est un pentagone régulier étoilé (ou « étoile à cinq branches ») que l’on peut inscrire dans un pentagone régulier.
- Un pentacle est la réunion d’un pentagone régulier et du pentagramme régulier de mêmes sommets que l’on peut y inscrire (page 9).
Pentamère (fleur)
Fleur présentant des pièces florales verticillées par cinq.
Pentastique
Disposé sur cinq rangs.
Pétale (n. m.)
Pièce florale de la corolle. Les pétales sont des feuilles modifiées, habituellement très visibles et pouvant être diversement colorés, qui entourent et protègent les étamines et le pistil, tout en servant de signal visuel pour les pollinisateurs.
Pétiole (n. m.)
Partie de la feuille reliant le limbe à la tige.
Photosynthèse (n. f.)
Processus biochimique, par lequel les plantes (mais aussi les algues et certaines bactéries) synthétisent, sous forme de sucres, de la matière organique. Avec de l’eau et la lumière solaire comme source d’énergie, les plantes absorbent puis dissocient des molécules de CO2 atmosphérique : elles conservent le carbone et rejettent une partie de l’oxygène libéré par la réaction.
Phyllotaxie (n. f.)
La phyllotaxie décrit la disposition des feuilles sur la tige d’un végétal.
Phytohormone (n. f.)
Hormone végétale, molécule produite par une plante et agissant à très faible dose. Parmi les phytohormones, les auxines, les cytokinines, les gibbérellines stimulent ou régulent la croissance ; l’acide abscissique a un effet inhibiteur ; l’éthylène intervient comme signal d’alarme de stress, mais aussi dans la maturation des fruits, etc.
Pièces florales
Définition extraite du Dictionnaire illustré de botanique (Jouy & de Foucault, 2016) : « les pièces florales sont les sépales, les pétales, les étamines et le(s) carpelle(s). Le carpelle est une pièce florale dérivant par modification d’une feuille et formée de l’ovaire contenant les ovules, du style et du stigmate. Le pistil, ou gynécée, est l’ensemble femelle de la fleur, formé par le(s) carpelle(s) ».
Pistil (n. m.)
Ensemble femelle de la fleur, formé d’un ou plusieurs carpelles.
Polaires (coordonnées)
En mathématiques, système de repérage dans le plan, défini par une demi-droite orientée et une mesure angulaire.
Dans ce système (figure 155), tout point M de coordonnées polaires ![]() est repéré par la longueur r du rayon vecteur et par l’angle
est repéré par la longueur r du rayon vecteur et par l’angle ![]() . Des calculs simples permettent de passer des coordonnées polaires aux coordonnées cartésiennes d’un point, et inversement, mais les équations des spirales sont bien plus simples en coordonnées polaires qu’en coordonnées cartésiennes.
. Des calculs simples permettent de passer des coordonnées polaires aux coordonnées cartésiennes d’un point, et inversement, mais les équations des spirales sont bien plus simples en coordonnées polaires qu’en coordonnées cartésiennes.
Polyèdre (n. m.)
En mathématiques, domaine fermé de l’espace, délimité par des polygones à côtés jointifs. Les cinq solides de Platon sont des polyèdres réguliers : tétraèdre (les quatre faces sont des triangles équilatéraux), cube (les six faces sont des carrés), octaèdre (les huit faces sont des triangles équilatéraux), dodécaèdre (les douze faces sont des pentagones), icosaèdre (les vingt faces sont des triangles équilatéraux).
Polygone, polygone régulier (n. m.)
En mathématiques, domaine fermé du plan, délimité par des segments de droites consécutifs. Les polygones les plus simples sont les triangles, les quadrilatères, le pentagone, l’hexagone, etc. Un polygone est régulier lorsqu’il est inscriptible dans un cercle, tout en ayant des côtés de même longueur.
Primordium / au pluriel primordia (n. m.)
En botanique, un primordium est un petit groupe de cellules qui se développera en feuille, en bourgeon, en fleur.
Principe de parcimonie
Le principe de parcimonie (aussi appelé « rasoir d’Ockham ») consiste à choisir, entre deux théories, celle qui donne l’explication la plus simple, tout en reposant sur les hypothèses à la fois les moins nombreuses et les plus simples. Pour autant, l’application de ce principe ne conduit pas nécessairement à la meilleure explication, qui peut être fondée sur d’autres hypothèses que celles envisagées.
Quadrature du cercle
Construction à la règle et au compas, recherchée en vain depuis l’Antiquité, d’un carré de même aire qu’un cercle donné. Le nombre π étant irrationnel (démonstration de Lambert, en 1761), cette construction est impossible. On peut cependant en donner une bonne approximation, en partant d’un triangle rectangle de côtés respectifs 3, 4, 5 (figure 156).
Construction de la figure 156 :
- construire le triangle ABC, rectangle en A, tel que AB = 4, AC = 3 et BC = 5 ;
- le cercle de centre A et de rayon AC coupe la droite (AB) en D tel que BD = 7 ;
- le cercle de centre B et de rayon BD (en pointillés « point-trait ») coupe la droite (AC) en E et F.
- par application du théorème de Pythagore dans le triangle ABE,
 ;
; - la longueur du côté du carré EFGH mesure
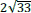 unités de longueur et son aire mesure 132 unités d’aire ;
unités de longueur et son aire mesure 132 unités d’aire ; - le cercle de centre A et de rayon AE coupe la droite (AB) en I ;
- d’après le théorème de Pythagore dans le triangle AIC rectangle en A,
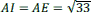 et AC = 3, et le rayon IC du cercle (c), tracé en rouge, mesure
et AC = 3, et le rayon IC du cercle (c), tracé en rouge, mesure  ;
; - en prenant 22/7 comme valeur approchée de π (voir page 4 et 5), l’aire A2 du cercle (c) mesure 132 unités d’aire, comme l’aire A1 du carré EFGH.
La quadrature du cercle est-elle réalisée ? Non : 22/7 n’est pas la valeur exacte de π, donc 132 n’est pas la mesure exacte de A2, bien que l’approximation soit excellente. La valeur de donnée par une calculatrice électronique est, au millième près le plus proche, égale à 131,946 unités d’aire. La différence entre cette valeur et 132 n’est que d’environ 0,05 unité d’aire.
La quadrature du cercle est l’archétype des problèmes dont l’énoncé est simple et compréhensible par tous, mais qui ont tenu en haleine les mathématiciens pendant des siècles. Si la quadrature du cercle est impossible à la règle et au compas, c’est quand même par des comparaisons d’aires que les mathématiciens grecs ont montré que l’aire d’un disque de rayon r est égale à πr². Une méthode consiste à découper le cercle en secteurs de même ouverture angulaire, puis à disposer ces secteurs tête-bêche pour former un pseudo-rectangle de même aire. Sur la figure 157 le disque de centre A est découpé en 36 secteurs circulaires de même angle au centre 10°. L’assemblage de ces secteurs donne un pseudo-rectangle ab1cd’2 de même aire que le disque.
Geogebra demande de nommer différemment deux points distincts d’une même figure : lorsqu’on passe du cercle de centre A au pseudo-rectangle ab1cd’2, le point A se retrouve en a et c, et le point B1 se retrouve en b1 et d’2.
Les lignes joignant a à d’2 et b1 à c paraissent droites sur la figure, mais elles sont formées de 18 arcs de cercles identiques et toutes deux ont pour longueur le demi-périmètre du disque. En augmentant le nombre des secteurs, donc en réduisant leur angle au centre, la précision s’améliore. À la limite, ab1cd’2 est un rectangle dans lequel ab1 = r et ad’2 = π : l’aire du disque de rayon r est égale à πr².
Quine (n. m.)
Suite de cinq mesures portées par la « canne des maîtres d’œuvre » du Moyen Âge. Le quine est gradué additivement (selon l’algorithme de Fibonacci) en paume, palme, empan, pied et coudée (pages 81 et 82).
Radian (mesure angulaire) (n. m.)
Le radian est la mesure d’un angle qui a pour sommet le centre d’un cercle et qui intercepte sur ce cercle un arc de longueur égale au rayon.
Un angle de 360° mesure 2π radians, un angle de 180° (angle plat) mesure π radians, un angle de 90° (angle droit) mesure π/2 radian, un angle de 72° mesure 2π/5 radian, un angle 60° mesure π/3 radian, un angle de 45° mesure π/4 radian, un angle de 30° mesure π/6 radian, etc.
Raisonnement par l’absurde
Raisonnement par lequel on montre qu’une proposition est vraie en prouvant que sa négation conduit à une contradiction. C’est par ce raisonnement que l’irrationalité de ![]() a été prouvée par l’école de Pythagore (voir détails sur Wikipedia). Ce raisonnement n’est utilisable qu’en logique binaire non contradictoire (celle des mathématiques et des ordinateurs), dans laquelle une proposition ne peut pas être indécidable : elle est soit vraie, soit fausse, chacune de ces valeurs de vérité excluant l’autre.
a été prouvée par l’école de Pythagore (voir détails sur Wikipedia). Ce raisonnement n’est utilisable qu’en logique binaire non contradictoire (celle des mathématiques et des ordinateurs), dans laquelle une proposition ne peut pas être indécidable : elle est soit vraie, soit fausse, chacune de ces valeurs de vérité excluant l’autre.
Rationnel (nombre)
En mathématiques, nombre entier ou s’exprimant comme quotient de deux nombres entiers : 3, 1/2, 4/5, etc.
Rayon vecteur (n. m.)
En mathématiques, pour tout point M du plan et dans un repère polaire d’origine O, longueur du segment [OM].
Rectangle d’or (voir pages 6 à 8)
Rectangle au format du nombre d’or, de longueur L et de largeur l telles que L/l = φ.
Récursif
Se dit d’une instruction informatique, d’un calcul (ou d’une construction géométrique) qui se répète indéfiniment à l’intérieur de lui-même, par itération d’une même règle.
Section dorée
Nom donné par Euclide à la division d’un segment en extrême et moyenne raison, qui définit le nombre d’or (voir page 3).
Sépale (n. m.)
Pièce florale du calice. Les sépales sont des feuilles modifiées (habituellement de couleur verte ou moins vive que celle des pétales) qui protègent la corolle, les étamines et le pistil lors du développement de la fleur.
Spirale (n. f.)
En mathématiques, courbe plane qui part d’un point central qui s’enroule autour de ce point tout en s’en éloignant. Parfois utilisé (à tort) pour désigner une hélice, courbe de l’espace dont la projection sur un plan perpendiculaire à son axe est une spirale.
Spirale d’Archimède
Spirale dans laquelle le rayon vecteur OM est proportionnel à la mesure de l’angle ![]() : l’écart radial entre deux spires est constant. L’équation polaire d’une spirale d’Archimède est de la forme r(t) = k x t, dans laquelle, pour tout point M, r est le rayon vecteur OM et t est l’angle
: l’écart radial entre deux spires est constant. L’équation polaire d’une spirale d’Archimède est de la forme r(t) = k x t, dans laquelle, pour tout point M, r est le rayon vecteur OM et t est l’angle ![]() .
.
Sur la figure 159 :
- pour aller du point A au point A’, a été augmenté de 1 radian (en valeur approchée 57,3°). Alors r’ = (t+1) / 10 = r + 1/10 ;
- les points M, M’, M », M »’, … sont alignés sur une demi-droite d’origine O. Pour aller du point M au point M’, t a été augmenté de 2π. Si le rayon-vecteur de M est égal à r, alors le rayon vecteur de M’ est égal à r’ = (t + 2π) /10 = t/10 + 2π/10 = r + π/5. De même, r » = r’ + π/5 et r »’ = r » + π/5 : les nombres r, r’, r » et r »’ sont les termes d’une suite arithmétique de premier terme r et de raison π/5 ≈ 0,63. En d’autres termes, MM’ = M’M » = M »M »’. Vérifiez-le expérimentalement en mesurant ces longueurs sur la figure. Percevez-vous l’illusion d’optique qui fait paraître MM’ plus long que M’M » et que M »M »’ ?
Cette propriété est générale : lorsque des points de la spirale d’équation r(t) = k x t sont alignés sur une demi-droite passant par O, leurs rayons vecteurs sont les termes d’une suite arithmétique de raison k x 2π.
Spirale du rectangle d’or
Spirale construite à la règle et au compas (figure 15) dans un rectangle d’or. Constituée d’arcs de cercles successifs, elle ne doit pas être confondue avec une spirale exponentielle, bien qu’elle en soit visuellement très proche (figure 19).
Spirale exponentielle
La spirale exponentielle – souvent appelée spirale logarithmique – a été définie et étudiée en 1792 par le mathématicien suisse Jacques Bernoulli. L’équation polaire d’une spirale exponentielle est de la forme r(t) = a x exp(b x t) ou, en notation classique r(t) = a x e(b x t). Dans cette équation et pour tout point M, r est le rayon vecteur OM et t est l’angle ![]() . Une telle spirale ne peut pas se construire à la règle et au compas (figures 17 et 18).
. Une telle spirale ne peut pas se construire à la règle et au compas (figures 17 et 18).
Lorsque des points d’une spirale exponentielle de centre O sont alignés sur une demi-droite d’origine O, leurs rayons vecteurs forment une suite géométrique de raison q = ebx2π. En effet, d’après les propriétés de l’exponentielle et pour deux tels points M et M’ alignés, OM = a x e(b x t) et OM’ = a x ebx(t+2π), donc OM’ = a x ebxt+bx2π = a x ebxt x q.
Sur la figure 160 :
- pour aller du point A au point A’, la valeur de t a été augmentée de 1 radian (en valeur approchée 57,3°). Alors
 et
et 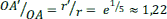 ;
; - Pour aller du point M au point M’, puis du point M’ au point M », la valeur de t a été augmentée de 2π radians. Alors OM’ = q et OM » = q² , avec q = e2xπ/5 ≈ 3,51.
Vérifiez-le expérimentalement en mesurant et en comparant ces rayons vecteurs sur cette figure.
Spirale générative
Spirale (ou hélice) le long de laquelle se forment les feuilles d’une plante, au sommet de la tige et en bordure du méristème. La spirale générative est habituellement peu visible : les spirales multiples qui apparaissent sur les feuilles, ou sur les fleurons d’un capitule, sont des parastiches.
Spiralée (phyllotaxie)
Phyllotaxie dans laquelle les feuilles alternes se répartissent sur une hélice entourant la tige.
Stipule (n. f.)
Appendice, habituellement double, situé de part et d’autre de la base du pétiole d’une feuille. Une stipule peut se réduire à une écaille (Ficus carica), ressembler à une petite feuille plus ou moins développée (de forme linéaire, triangulaire, arrondie, dentée ou non, laciniée, parfois enveloppante, etc.) ou même être épineuse (Robinia pseudoacacia), etc.
Suite numérique (n. f.)
En mathématiques, relation qui, à chaque nombre entier naturel n, associe un unique élément un, appelé terme d’indice n et dont la valeur se calcule en fonction de n. Par exemple, les suites définies par un = 2n et νn = 2n + 1, avec n ≥ 0, ont pour termes respectifs 0, 2, 4, 6, 8… (suite des nombres entiers naturels pairs) et 1, 3, 5, 7, 9… (suite des nombres entiers naturels impairs).
Suites numériques particulières :
- Suite arithmétique : suite numérique définie par son premier terme u0 et la relation récurrente un+1 = un + r, dans laquelle r est un nombre constant appelé raison.
- Suite géométrique : suite numérique définie par son premier terme u0 et la relation récurrente un+1 = un x q, dans laquelle q est un nombre constant appelé raison.
- Suite récurrente : suite dans laquelle un terme se calcule en fonction d’un ou plusieurs de ses termes précédents.
- Suite récurrente linéaire d’ordre 2 : suite définie par une relation récurrente du type un+2= a x un+1 + b x un, dans laquelle a et b sont deux nombres fixés, et par la valeur de ses deux premiers termes.
- Suite de Fibonacci : la plus simple des suites récurrentes linéaires d’ordre 2, définie par la relation récurrente un+2 = un+1 + un avec u0 = 1 et u1 = 1. Les termes suivants sont u2 = 2, u3 = 3, u4 = 5, u5 = 8, etc.
Tépales (n. m.)
Désigne des sépales et des pétales semblables par leur forme, leur taille et leur couleur, ce qui les rend difficiles à distinguer les uns des autres (figure 51).
Tétramère (fleur)
Se dit d’une fleur présentant des pièces florales verticillées par quatre.
Tétrastique
Disposé sur quatre rangs.
Théorème de Pythagore et sa réciproque
Célèbre théorème, qui caractérise un triangle rectangle par la mesure de ses côtés. Avec les notations de la figure 161 :
- si le triangle ABC est rectangle en A, alors a² = b² + c² ;
- réciproquement, si a² = b² + c², alors le triangle ABC est rectangle en A.
Un triplet (a, b, c) de nombres entiers naturels est pythagoricien lorsqu’il vérifie la relation a² = b² + c².
Ce théorème, bien qu’attribué à Pythagore (580 à 495 av. J.-C.), était connu de manière empirique depuis la plus haute antiquité. Sa première démonstration connue (donnée par Euclide dans ses Éléments, aux environs de 300 av. J.-C.) repose sur des comparaisons d’aires et non sur des calculs de longueurs.
Le théorème de Pythagore permet de calculer la longueur d’un côté d’un triangle rectangle connaissant la longueur des deux autres. Mais, dans l’antiquité, il servait essentiellement à construire des angles droits, pour l’arpentage et la construction de bâtiments, à l’aide d’une corde à treize nœuds. Sur celle-ci, les treize nœuds régulièrement espacés délimitent douze intervalles de même longueur : puisque 12 = 3 + 4 +5 et 3² + 4² = 5², le triangle de côtés 3, 4, 5 est un triangle rectangle.
Trimère
Se dit d’une fleur présentant des pièces florales verticillées par trois.
Tristique
Disposé sur trois rangs.
Variable numérique
Nombre pouvant prendre différentes valeurs dans un ensemble donné, par opposition à un paramètre, dont la valeur fixe les conditions initiales d’un calcul.
Verticille (n. m.)
Groupe de plus de deux feuilles (ou pièces florales) sur un même nœud.
Verticillées
Se dit de feuilles, ou de pièces florales, groupées en verticilles.
Volubile
Se dit d’une plante grimpante, dont la tige s’enroule en hélice sur son support.
Vrille (n. m.)
Organe permettant à un végétal (vigne, bryone, pois, gesses, vesces, etc.) de s’accrocher, en s’enroulant en hélice sur la végétation environnante ou sur d’autres supports.
Sur la figure 162, un rameau mort a été placé au contact de la vrille de Bryonia dioica, qui était initialement à peu près rectiligne. Successivement et de gauche à droite : au bout de 10 minutes, 30 minutes, 45 minutes, 60 minutes. Au bout de deux heures, la vrille avait terminé un deuxième tour et enserrait fortement son support. Pour cela, la torsion se propage (au-delà du point de contact initial et dans le sens de l’enroulement) vers l’extrémité de la vrille, bien que celle-ci soit libre.
Sur la figure 163, deux jours plus tard, la vrille a fait quatre tours autour du rameau auquel elle s’est initialement enroulée et elle a formé, de part et d’autre des deux points blancs, des hélices de sens opposés, faisant office de tendeurs élastiques entre la tige et son support. Comptez les spires de chaque sens : leur nombre est équilibré, et cette propriété se retrouve (habituellement à une spire près) sur toutes les vrilles de bryone observées sur différents pieds. Au final, la torsion de la vrille, contrainte à chacune de ses extrémités, est locale et non globale. Étonnant…, mais comment expliquer la formation de ces remarquables ressorts hélicoïdaux ? Encore une invention de l’évolution qui ne doit rien à l’intelligence humaine.
Zodiaque (n. m.)
Le zodiaque est un bandeau circulaire porté par la sphère céleste et centré sur le plan écliptique, qui contient l’orbite de la Terre autour du Soleil. Depuis l’Antiquité, le zodiaque astrologique est traditionnellement partagé en douze secteurs de 30°, contenant chacun une constellation associée à un signe astrologique. Lorsque l’année commençait au moment de l’équinoxe de printemps (qui se produit le plus souvent le 20 mars, rarement le 21 mars, exceptionnellement le 19 mars), les signes du zodiaque correspondaient, dans le même ordre, aux douze mois de l’année. Alors les mois de septembre, octobre, novembre, décembre étaient respectivement les 7e, 8e, 9e et 10e mois, comme l’indique leur racine latine.
La figure 164 compare les mois de l’année (couronne noire) aux dates des signes du zodiaque, tels que décrits par l’astrologie occidentale (couronne rouge), et aux dates actuelles d’observation des constellations astronomiques dans le zodiaque (couronne verte). Pour simplifier la figure et avec une erreur moyenne inférieure à 1° d’arc, les mois de l’année et les signes astrologiques occupent des secteurs de même ouverture angulaire 30°.
Cette figure amène deux remarques :
- Les constellations n’apparaissent pas aux dates données par les astrologues. Ces dates, inchangées depuis environ 2 400 ans, ne tiennent pas compte de la précession des équinoxes. Comme celui d’une toupie légèrement déséquilibrée, l’axe de rotation de la Terre se déplace lentement, de manière périodique, et le zodiaque tourne sur lui-même en 26 000 ans environ. Le décalage actuel est proche de un mois : pendant les jours qui suivent l’équinoxe de printemps, les prévisions astrologiques devraient être rapportées au signe des Poissons, et non à celui du Bélier. Mais cela n’empêche pas certains astrologues de faire des calculs de position des planètes selon leur tradition et… « à la seconde près » !
- Les constellations, groupes d’étoiles délimités de manière plus ou moins arbitraire et de dimensions différentes, ne sont pas nécessairement au nombre de douze et n’occupent pas des secteurs de même ouverture angulaire. Le signe astrologique de la Vierge devrait durer environ deux fois plus longtemps que celui de la Balance, et celui du Lion devait durer environ 2,2 fois plus longtemps que celui du Cancer.
Croyance scientifiquement infondée, l’astrologie reste un bon exemple des interprétations que donnaient les peuples de l’Antiquité de leur perception du monde. L’humanité arrivera-t-elle un jour à considérer que son avenir est entre ses mains – plutôt que dans une fatalité magique qui serait inscrite dans les astres – et que le hasard est l’un des moteurs de l’évolution ?
Bibliographie
APMEP (Association des professeurs de mathématiques de l’enseignement public), 2000. Brins d’histoire des Maths, Galion thème n° 2 – Unités de mesure à travers les âges. https://apmep.fr/GALION-Themes [16 juillet 2020].
Bell A.-D. & Bryan A., 1991 (réédition 2008). Plant form, an illustration guide to flowering plant morphology. Timber Press, Portland, London, 431 p.
Besnard F., 2011. Rôle des AHP6 dans le contrôle de la phyllotaxie… Thèse, ENS Lyon, https://scanr.enseignementsup-recherche.gouv.fr/publication/these2011ENSL0638 [16 juillet 2020].
Boissière S., 2000. Dynamique de la phyllotaxie. http://ww-math.sp2mi.univ-poitiers.fr>publications [16 juillet 2020].
Corbalán F., 2010. Le nombre d’or, le langage mathématique de la beauté. RBA Coleccionables, Barcelone, 158 p.
Debart P., 2003, mise à jour 7 janvier 2020. Descartes et les mathématiques. https://debart.pagesperso.orange.fr [16 juillet 2020].
Delahaye J.-P., 2020. Dans les arcanes des triplets pythagoriciens. Pour la Science 514 : 80-85.
Dumont E., 2014. La géométrie dans le monde végétal. Ulmer, Paris, 191 p.
I.R.E.M. de Strasbourg, 2002. Spirales végétales et suite de Fibonacci, un atelier mathématique pour les enfants. http://numerisatio.univ-irem.fr/AAA/AAA04076/AAA04076.pdf [16 juillet 2020].
Jean R.V., 1983. Croissance végétale et morphogenèse. Masson, Paris, Presse de l’Université du Québec, Québec, 322 p.
Jouy A. & de Foucault B., 2016. Dictionnaire illustré de botanique. Biotope, Mèze, 471 p.
Livio M., 2018. Le nombre d’or, les clés du mystère. Odile Jacob, Paris, 310 p.
Loiseau J.E., 1969. La phyllotaxie. Masson, Paris, 223 p.
Pacioli L. & de Vinci L., 1509. De Divina proportione. Fac-similé de l’édition originale, édition 2014, Léopold, Marseille, 322 p.
Rousseau C. & Zazoun R., 2008. Spirales végétales. Dossier Accromath/volume III/été automne 2008, p. 12 à 18. https://accromath.uqam.ca/volume/volume 3-2-2008 [16 juillet 2020].
Rowe-Pirra W., 2019. Une disposition des feuilles qui dépend de leur âge. Pour la Science 502 : 16.
Tison J.-M. & de Foucault B. (coords), 2014. Flora gallica. Flore de France. Biotope, Mèze, xx + 1 196 p.
Tison J.-M., Jauzein Ph. & Michaud H., 2014. Flore de la France méditerranéenne continentale. Naturalia publications, Turriers, 2 077 p.
Vernoux T., Godin C. & Besnard F., 2018. Quand les plantes font des maths. Pour la Science, hors-série, 101 : 51-58.
Vincent R., 2015. Géométrie du nombre d’or. Chalagam Éditions, 127 p.
Remerciements
Cette étude sur le nombre d’or m’a été suggérée par Robert Pistre, qui me connaissait en tant que botaniste amateur et professeur de mathématiques, et qui était intrigué par les liens entre le nombre d’or et la botanique.
Mes plus vifs remerciements à Raymond Jean, professeur de botanique honoraire à l’université de Lille, pour ses conseils et son aide précieuse dans la partie phyllotaxie, à Bruno David, qui m’a incité à publier cet article, et à Bruno de Foucault, pour sa relecture et sa mise en page.
Merci au Conservatoire botanique Pierre-Fabre et à la Jardinerie tarnaise, grâce auxquels j’ai pu photographier des plantes des déserts présentant de rares phyllotaxies.